How do you determine if there is a significant relationship between two variables with several factors affecting it, using R?

Question

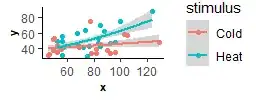
I want to check if there is a significant relationship between x and y, and then check if this relationship is affected by different stimuli (2 levels), colonies (2 levels), and lightings situation (2 levels).

Which statistical test should I apply?

bellow is my sample dataset:

Colony means that individuals are coming from different mothers.

The hypothesis is that under different lighting conditions (whether light or dark), the result will not change.

In this example x is the number of successes during training _ all subjects (ID) have got a specific amount of time (like 10 hours) to do a task, one individual could do it 100 times during the given time, and the other could do only 60 times for example. For y, which is the number of successes during the memory test, all subjects (ID) got a specific amount of time (like 5 hours) to do the task, again one individual did the task 50 times during the given time while another did it only 20 times. So training (x) was done for 10 hours, but the memory (y) was tested for 5 hours, but the timing was the same for all individuals (ID), the number of successes could be as much as an individual is willing to do the task.

df <- structure(list(ID=c(1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40),
                     colony=c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2),
                     stimulus=c("Heat","Heat","Heat","Heat","Heat","Heat","Heat","Heat","Heat","Heat", "Cold","Cold","Cold","Cold","Cold","Cold","Cold","Cold","Cold","Cold","Heat","Heat","Heat","Heat","Heat","Heat","Heat","Heat","Heat","Heat", "Cold","Cold","Cold","Cold","Cold","Cold","Cold","Cold","Cold","Cold"),
                     lighting=c("light","light","light","light","light","dark","dark","dark","dark","dark","light","light","light","light","light","dark","dark","dark","dark","dark","light","light","light","light","light","dark","dark","dark","dark","dark","light","light","light","light","light","dark","dark","dark","dark","dark"),
                     x=c(124,  73,  83,  85,  67, 100,  56,  88,  76,  68, 105,  92,  85, 103, 129,  90, 82,  82,  78,  96,  83,  92,  57,  52,  56,  75,  96,  85,  72,  56,  50,  69, 45,  49,  52,  46,  49,  52,  55,  77),
                     y=c(89, 63, 46, 70, 60, 75, 30, 62, 42, 44, 57, 33, 45, 58, 47, 37, 33, 38, 33, 35, 53, 46, 41, 49, 55, 29, 47, 43, 41, 49, 53, 41, 31, 37, 35, 32, 51, 44, 38, 75)), 
                class = "data.frame", row.names = c(NA,-40L))

And the main question is whether the number of successes during memory has any relationship to the number of successes during the training (so does having more success during training leads to more success during memory?)

Answer 1

I presume that you want to know whether the linear relation between $x$ and $y$ is different depending on those additional variables, which I also presume to not be confounders. Thus, you don't want to control for them but you rather want to learn their interaction with the treatment $x$.

If that is all true, use as formula for 'lm': $$ y \sim x \;+\; \mbox{stimulus}:x \;+\; \mbox{colony}:x \;+\; \mbox{lighting}:x $$ and the p-values of the coefficients of the interaction terms, given by the model fitted by lm, will then tell you whether those interactions are significant.

To make it more complicated, you could also think about higher-order interactions like $x$:stimulus:colony.

---

Edit:
And I agree with @dipetkov's point below that, at least in general in those situations, we should also include an offset for the interactions. This was an omission on my side.

Answer 2

I disagree with @frank's advice to include interactions (with $x$) but no main effects for the stimulus, lighting and colony variables. But see How do you deal with "nested" variables in a regression model? for an important exception to this rule.

Moreover, a scatterplot of the data reveals that the two colonies are observed under different conditions. The difference is most pronounced when stimulus = "Cold" as there is complete separation in the $x$ values. (This may indicate that $x$ is not really a "treatment" assigned randomly to units as @frank interprets it.) This pattern suggests to interact colony with all the other variables, which leads — visually at least — to a better model fit.

Update: The OP has provided additional context. The experimental design is still unclear but it seems the units were randomized to one of four conditions (stimulus×lighting), given time to train under the assigned condition (x), and then tested "officially" (y). The numerical variables x and y are number of successfully completed tasks in a fixed amount of time (everyone got the same amount of time). The number of attempted but unsuccessful tasks is ignored though it may be important: what if stimulus and lighting affect the number of trials but not the success rate of a trial?

Also unexplained is the concept of a colony. The number of successes x during training under Cold stimulus is markedly different for colonies 1 and 2. On its own, the data cannot explain why this happened and therefore the data cannot point out which is the most scientifically justified model either. Instead the OP should explain/examine the difference between the two colonies. If these two colonies were sampled from a larger population, it would help to do followup experiments to investigate the variability between colonies under "Cold" stimulus. If these two colonies are the only ones of interest, it would help to sample more units from each colony to study the variability within each colony.

To highlight the importance of colony and following comments by @SextusEmpiricus, let's compare two model fits: the full model y ~ x * stimulus * lighting * colony (figure above) and the restricted model y ~ x * stimulus * lighting (figure below). The full model fits better statistically (in terms of an F-test). As it fits a regression line for each stimulus×lighting×colony combination, the full model interpolates well "unusual" points. I've highlighted one such point in each panel without testing formally that these points are outliers or high-leverage. The restricted model fits a line for the four stimulus×lighting combinations (four panels) and — within each panel — it uses the same line for the two colonies. Qualitatively, the fit is not bad and I can come up with a nice story that training is effective (the regression lines have positive slopes) under all conditions except for "dark and cold". Whether this story is meaningful depends on what the colonies actually are.

---

Here is R code to reproduce the figures and play with different models for this data.

library("broom")
library("tidyverse")
Cast colony and ID as categorical (rather than numeric) variables.
df <- as_tibble(df) %>%
  mutate(
    colony = as.character(colony)
  )
outliers <- c(1, 6, 15, 40)
extract_model_formula <- function(model) {
  Reduce(paste, deparse(model$call$formula))
}
plot_model_fit <- function(model, title = "") {
  model %>%
    augment(
      newdata = df
    ) %>%
    ggplot(
      aes(x, .fitted)
    ) +
    geom_line(
      aes(color = colony)
    ) +
    geom_text(
      aes(x, y,
        color = colony,
        label = colony
      ),
      data = df,
      inherit.aes = FALSE
    ) +
    geom_label(
      aes(x, y,
        color = colony,
        label = colony
      ),
      data = df %>% filter(ID %in% outliers),
      inherit.aes = FALSE
    ) +
    facet_grid(
      stimulus ~ lighting
    ) +
    theme(
      plot.title = element_text(
        size = 12
      ),
      legend.position = "none"
    ) +
    ggtitle(
      title, extract_model_formula(model)
    )
}
m0 <- lm(
  y ~ x + x:stimulus + x:lighting + x:colony,
y ~ x + x:(stimulus + lighting + colony),
data = df
)
plot_model_fit(
  m0,
  "Interactions without main effects is often not a great choice."
)
m1 <- lm(
  y ~ x * stimulus * lighting * colony,
  data = df
)
plot_model_fit(
  m1,
  "For each variable interacted with x, include its main effect as well."
)
m2 <- lm(
  y ~ x * stimulus * lighting,
  data = df
)
plot_model_fit(
  m2,
  "What is a colony and should it be included in the model? This is a domain knowledge question."
)
anova(m1, m2)
```

Answer 3

We assume that the question is how to determine whether stimulus is statistically significant in the presence of the other variables. First let us try a mixed model with colony as a random effect. Unfortunately, using the data in the question, this results in a singular model which can also be seen from the zero random effects. This is suggestive of overfitting.

library(lmer)
fm1 <- lmer(y ~ x + stimulus + lighting + (1|colony), df)
## boundary (singular) fit: see help('isSingular')
ranef(fm1)
$colony
(Intercept)
1           0
2           0

Thus we try a fixed effects model. We can try interactions among all variables

fm2 <- lm(y ~ x * stimulus * lighting * colony, df)
summary(fm2)

giving:

Call:
lm(formula = y ~ x * stimulus * lighting * colony, data = df)
Residuals:
    Min      1Q  Median      3Q     Max 
-17.742  -3.199   0.721   4.297  14.172
Coefficients:
                                     Estimate Std. Error t value Pr(>|t|)

(Intercept)                           73.1768   101.9931   0.717   0.4800

x                                     -1.0131     1.2157  -0.833   0.4128

stimulusHeat                        -172.2299   111.4630  -1.545   0.1354

lightinglight                        -45.0352   117.2821  -0.384   0.7044

colony                               -46.2449    53.7372  -0.861   0.3980

x:stimulusHeat                         3.0552     1.3429   2.275   0.0321 *
x:lightinglight                        1.1976     1.3931   0.860   0.3985

stimulusHeat:lightinglight           132.2606   131.0734   1.009   0.3230

x:colony                               1.1097     0.6769   1.639   0.1142

stimulusHeat:colony                  117.2380    61.3083   1.912   0.0678 .
lightinglight:colony                  46.8192    64.6041   0.725   0.4756

x:stimulusHeat:lightinglight          -2.1497     1.5701  -1.369   0.1836

x:stimulusHeat:colony                 -2.1382     0.7744  -2.761   0.0109 *
x:lightinglight:colony                -1.1066     0.8541  -1.296   0.2074

stimulusHeat:lightinglight:colony    -87.6013    74.7980  -1.171   0.2530

x:stimulusHeat:lightinglight:colony    1.5915     0.9806   1.623   0.1176

Signif. codes:  0 ‘*’ 0.001 ‘’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 8.473 on 24 degrees of freedom
Multiple R-squared:  0.767,     Adjusted R-squared:  0.6214 
F-statistic: 5.268 on 15 and 24 DF,  p-value: 0.0001652

Looking at which coefficients are significant (marked to the right of the p values) it seems that we can simplify the model by omitting lighting. Comparing that to the same model without stimulus we have a highly significant difference between the models with stimulus and without (p = 1.839e-05).

fm3 <- lm(y ~ x * stimulus * colony, df)
fm4 <- lm(y ~ x * colony, df)
anova(fm4, fm3)
## Analysis of Variance Table
##
## Model 1: y ~ x * colony
## Model 2: y ~ x * stimulus * colony
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1     36 6053.3                                  
## 2     32 2651.9  4    3401.4 10.261 1.839e-05 ***
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Here is a plot of x on horizontal axis vs y on vertical axis with separate panels for the colonies. The colors represent the stimulus.

library(lattice)
xyplot(y ~ x | factor(colony), df, groups = stimulus, 
  type = c("p", "r"), auto = TRUE)