First let's look at the data to gain a bit of understanding about the problem.
data
#> # A tibble: 236 × 4
#> PARTICIPANT X1 X2 SCORE
#> <chr> <dbl> <chr> <dbl>
#> 1 1 26.6 Test1 21
#> 2 1 26.6 Test2 NA
#> 3 2 88.4 Test1 21
#> 4 2 88.4 Test2 20
#> 5 3 NA Test1 15
#> 6 3 NA Test2 17
#> 7 4 NA Test1 26
#> 8 4 NA Test2 19
#> 9 5 76.4 Test1 52
#> 10 5 76.4 Test2 21
#> # … with 226 more rows
So this is test score data for two tests, Test1 and Test2, and X1 is a participant-level predictor.
Quite a bit of data is missing, esp. in the X1 predictor which is missing for 38 out of 118 (32%) participants. There are some missing test scores as well.

Without imputation (which would be challenging with only X1 and the scores), we lose 37% of the observations (rows) because of NA's. Of the remaining 80 participants, 12 participants (15%) have only their Test1 score; their Test2 is missing. This is important because it's difficult to estimate a participant random effect with just one observation from a participant.
In fact, you should be very careful about the missing data and account for it, as some of it (the missing Test2 score in particular) may not be missing at random.
Now let's make some plots.
To start with, the Test1 and Test2 scores have very different distributions. Keep in mind that X1 cannot explain these differences because X1 is a participant-level predictor, not a test-level predictor.


I see a strong linear correlation between the Test1 and the Test2 score of a participant. But the range of the Test1 scores seems to be [0, 120] while the range of the Test2 scores seems to be [0, 60]. Now I have follow-up questions about whether the two tests are even measuring the same thing and how comparable Test1 and Test2 score are...
Next I plot the score as a function of the continuous predictor X1 and I add two smooth (loess) curves, to help me get an idea what model might be appropriate for this data.

We learn a lot from plot, though it's mostly not good news.
- The relationship between X1 and SCORE is not really linear: Higher X1 is associated with higher SCORE when X1 < 40 or X1 > 80 (or so). In the mid-range 40 ≤ X1 ≤ 80 the curve are flat (there doesn't seem to be a relationship).
- The variance in Test1 is higher (about twice as high?) as the variance in the Test scores. Your current model assumes constant variance, so cannot model this pattern in the variability of test scores.
Based on these observations, I decide to fit a linear model using Generalized Least Squares (GLS).
- I use restricted cubic splines (with 4 knots) to model the non-linear relationship between X1 and SCORE.
- I don't interact X1 and X2 because the shape of the curves isn't that different. It seems enough to have different intercepts for the two tests, effectively shifting Test1 scores "up" compared to Test2 scores.
library("rms")
dd <- datadist(data)
options(datadist = "dd")
model <- Gls(
SCORE ~ rcs(X1, 4) + X2,
data = data,
correlation = corSymm(form = ~ 1 | PARTICIPANT),
weights = varIdent(form = ~ 1 | X2)
)
ggplot(Predict(model, X1, X2))

anova(model)
#> Wald Statistics Response: SCORE
#>
#> Factor Chi-Square d.f. P
#> X1 19.09 3 0.0003
#> Nonlinear 4.68 2 0.0962
#> X2 68.77 1 <.0001
#> TOTAL 86.25 4 <.0001
The model does explain some of the variability in test scores. But the non-normality is still present.

And the heteroscedasticity (the residual variance increases with the response) is also still present.
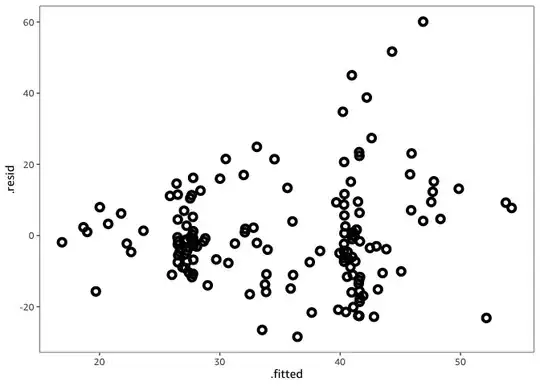
There might be nothing we can do about this however: the residual variance is not a function of X1.
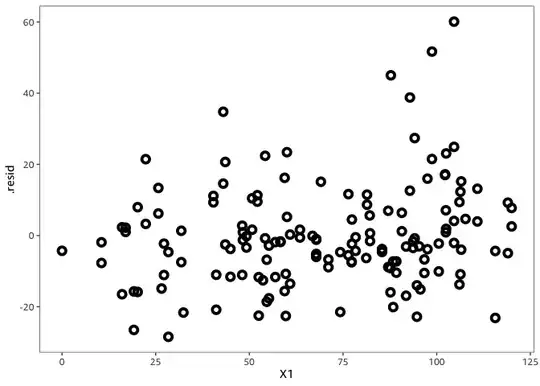
Log-transforming the scores as suggested by @Lachlan helps with the heteroskedasticity since the log is a variance stabilizing transformation; the QQ plot looks "more Normal". However, it cannot help with the fact that there isn't much of a relationship between X1 and test scores, except for "extreme" X1 values (very low X1 or very high X1).
The R code to reproduce the figures and the analysis:
library("naniar")
library("rms")
library("nlme")
library("tidyverse")
data <-
here::here("data", "588224.csv") %>%
read_csv(
col_types = cols(PARTICIPANT = col_character())
) %>%
rename(
X1 = X1_notCentered
) %>%
select(
PARTICIPANT, X1, X2, SCORE
)
data
data %>%
pivot_wider(
id_cols = c(PARTICIPANT, X1),
names_from = X2,
values_from = SCORE
) %>%
select(
-PARTICIPANT
) %>%
vis_miss()
data <- drop_na(data)
data %>%
pivot_wider(
id_cols = c(PARTICIPANT, X1),
names_from = X2,
values_from = SCORE
) %>%
ggplot(
aes(
Test1, Test2,
color = X1
)
) +
geom_point(
shape = 1,
size = 2,
stroke = 2
) +
scale_x_continuous(
limits = c(0, 120)
) +
scale_y_continuous(
limits = c(0, 60)
)
data %>%
ggplot(
aes(SCORE, fill = X2)
) +
geom_histogram(
bins = 33,
alpha = 0.5
) +
scale_x_continuous(
limits = c(0, 120)
)
Log-transform the test scores?
data <- data %>%
mutate(
# No:
# Y = SCORE,
# Yes:
Y = log2(SCORE)
)
data %>%
ggplot(
aes(
X1, Y,
color = X2,
shape = X2,
group = X2,
fill = X2
)
) +
geom_smooth(
show.legend = FALSE
) +
geom_point(
size = 2,
stroke = 2
) +
scale_shape_manual(
values = c(1, 2)
)
dd <- datadist(data)
options(datadist = "dd")
model <- Gls(
Y ~ rcs(X1, 4) + X2,
data = data,
correlation = corSymm(form = ~ 1 | PARTICIPANT),
weights = varIdent(form = ~ 1 | X2)
)
ggplot(Predict(model, X1, X2))
anova(model)
data <- data %>%
mutate(
.fitted = fitted(model),
.resid = resid(model)
)
data %>%
ggplot(
aes(sample = .resid)
) +
stat_qq() +
stat_qq_line() +
theme(
aspect.ratio = 1
)
data %>%
ggplot(
aes(
.fitted, .resid,
color = X2
)
) +
geom_point(
size = 2,
shape = 1,
stroke = 2
)
data %>%
ggplot(
aes(
X1, .resid,
color = X2
)
) +
geom_point(
size = 2,
shape = 1,
stroke = 2
)










shapiro.test(resid(mod1))? What should I use instead to get the model's residuals? (I'm used to lm$residuals, but it doesn't seem to work with lmer) – Larissa Cury Sep 09 '22 at 01:50