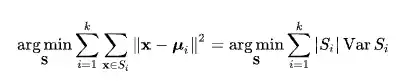Wikipedia gives one formulation for the k-means problem as:
where we intend to find a set of clusters $S = \{S_1, \ldots, S_k\}$ to minimize this value. However, the equivalent formulation
divides the sum of pairwise distances by the size of the cluster. Intuitively, why does the first formulation (using sum of distances from center) not divide by the size of the cluster as well, while the second one does?
Intuitively, it is because the second sum has many more summands.
To be precise, we have to show that for all $i=1,\ldots,k$: $$ \frac{1}{|S_i|}\sum_{x, y\in S_i}\|x - y\|^2 = \sum_{x\in S_i}\|x-\mu_i\|^2. $$ But, using the identity: $$ \sum_y\|x - y\|^2 = \|x-\mu_i\|^2 + \sum_{y\ne x}\|\mu_i-y\|^2, $$ which is just Pythagoras, we get: $$ \begin{align} \sum_{x, y\in S_i}\|x - y\|^2 &= \sum_{x}\left[ \|x-\mu_i\|^2 + \sum_{y\ne x}\|\mu_i-y\|^2\right]\\ &= \sum_x \sum_y\|\mu_i-y\|^2\\ &= |S_i|\sum_y\|\mu_i-y\|^2, \end{align} $$ which is what we wanted to show.
