General form of the distribution of distances to a fixed point in rectangle

Question

The answer given to the question Probability distribution of the distance of a point in a square to a fixed point solves for the "distribution of the distance between the origin (0,0) and a random point on the unit square $(0,1)^2$".

Can this be generalized to a rectangle of arbitrary lengths and a random origin within it?

Edit: the article Distribution of Distances between Elements in a Compact Set apparently does this (I think?) but the math is not trivial and I can not be sure.

Answer 1

Let the rectangle have dimensions $w \le h.$ Place two of its vertices at $(0,0)$ and $(w,h)$ in a Cartesian coordinate system and let the central point be at $(x,y)$ with $0\le x \le w$ and $0\le y \le h.$ The vertical line through $x$ and the horizontal line through $y$ divide this rectangle into subrectangles of areas $xy,$ $x(h-y),$ $(w-x)y,$ and $(w-x)(h-y).$ The mean distance to $(x,y)$ is the average mean distance within each of these subrectangles, weighted by their relative areas.

Scale everything by a factor of $1/w$ to make the rectangle of unit width: the answer will be multiplied by $w$ to account for this scale. That reduces the problem to the case $(x,y)=(0,0)$ and $(w,h) = (1,h).$ The chance that the mean distance is less than any radius $r$ is proportional to the area of the rectangle within the circle of radius $r.$ Here are three typical configurations:

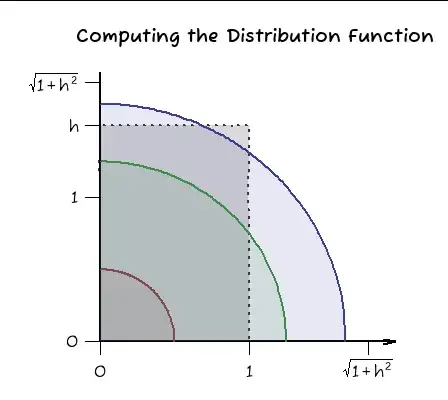
If we let $s(x, r)$ be half the area of the segment of a semicircle of radius $r$ above a height of $x \ge 0,$ geometry tells us that when $x \ge r,$ $s(x,r)=0$ and otherwise

$$s(x,r) = \frac{1}{2}\left( \theta r^2 - x \sqrt{r^2 - x^2}\right)$$

where $\theta = \arccos(x/r)$ is the angle subtended by the entire segment. There are generally two such half-segments in this figure (one or both of which might be empty), illustrated by the portions of the largest blue circle at the right and above the rectangle. They have areas $s(1,r)$ and $s(h,r),$ respectively. Subtracting them from the area of this quarter circle, $\pi r^2/4,$ yields the area remaining inside the rectangle. Dividing this by the rectangle's area $h$ gives the desired probability, as plotted here. The colors correspond to the regimes illustrated in the previous figure.

Thus, the general solution is a mixture of four such distributions weighted by the subrectangle areas.

---

The mean distance, to illustrate, is

$$\begin{aligned} &\frac{1}{h}\int_0^h \int_0^1 \sqrt{u^2 + v^2}\,\mathrm d u \mathrm d v \\ &= \frac{d}{3} + \frac{\log(h+d)}{6h} + h^2\left(\frac{\log(h)}{12} - \frac{\log(d-1)}{8} + \frac{\log(d+1)}{24}\right) \end{aligned}$$

where $d = \sqrt{1 + h^2}$ is the diameter of the rectangle.

Here is a tested R implementation of the distribution function to a vertex of a rectangle (of unit width and height h).

#
# Area of half a circular segment in a circle of radius `r` above a height of `h`.
#
segment <- function(h, r = 1) {
  ifelse(h >= r, 0, {
           a <- acos(pmin(1, h / r)) # The included angle
           (a * r^2 - h * sqrt(pmax(0, r^2 - h^2))) / 2
  })
}
#
# Distance distribution function.
# Vectorized over `r`.
#
ff <- function(r, h) {
Reduce to the case h >= 1.
h <- abs(h)
  if (isTRUE(h < 1)) {
    r <- r / h^2
    h <- 1 / h
  }
Clamp r to the support of the distribution.
r <- pmax(0, pmin(sqrt(1 + h^2), r))
Apply the formula.
(pi * r^2 / 4 - segment(1, r) - segment(h, r)) / h
}

To illustrate the process of computing an area-weighted average, here is an implementation of the mean to any interior location in a rectangle.

#
# Works *only* for 0 <= x <= w and 0 <= y <= h.
# Parallelized.
#
g <- function(x, y, w, h) {
  #
  # The basic formula for integrated distance to the origin.
  #
  f <- function(h) {
    u <- sqrt(1 + h^2)
    (log(h + u)/(6 * h) + u / 3 + h^2 * (log(h) / 12 - log(u - 1)/8 + log(u + 1)/24))
  }
  #
  # Mean distance scaled by the rectangle's area.
  #
  f2 <- function(h, w = 1) 
    ifelse(h * w > 0, f(h / w) * w^2 * h, 0)
  #
  # Area-weighted average of mean distances.
  #
  (f2(y, x) + f2(h-y, x) + f2(y, w-x) + f2(h-y, w-x)) / (w * h)
}

For testing, you may compare its output to a Monte-Carlo simulation:

g.sim <- function(x, y, w, h, N = 1e3) {
  sqrt(colSums((matrix(runif(2 * N, 0, c(w, h)), 2) - c(x, y))^2))
}

g.sim returns N distances, which you may use to estimate the entire distribution (compare that to ff) or any of its properties such as the mean distance (compare that to g).

The simulation automatically handles the general case where $(x,y)$ is not necessarily in the interior of the rectangle.

The formulas for the distribution and its mean can be extended to the general case by expressing the problem as a weighted average where some of the weights (for rectangles outside the original one) are negative. I leave that to the interested reader to devise -- no new ideas or formulas are needed.