I've fitted a mixed model with participants and vowels as random factors and language (Tamil and French) as the fixed factor. The dependent variable is durations of prolongations (of a phoneme). The question I'm trying to answer: are the mean durations of prolongations in the two language significantly different from one another? I considered a T-test, but realized that it may not capture the effects of variations in the population or even vowels (some vowels in english or german are more easily prolonged than consonants, for example).
model1<-lmer(log(Duration) ~ Language + (1|Participant) + (1|Vowel), data = lmmdf, REML = TRUE)
summary(model1)
Output:
Linear mixed model fit by REML. t-tests use Satterthwaite's method
[lmerModLmerTest]
Formula: log(Duration) ~ Language + (1 | Participant) + (1 | Vowel)
Data: lmmdf
REML criterion at convergence: 363.8
Scaled residuals:
Min 1Q Median 3Q Max
-3.03238 -0.65717 -0.05817 0.67908 2.42541
Random effects:
Groups Name Variance Std.Dev.
Vowel (Intercept) 0.030179 0.17372
Participant (Intercept) 0.009809 0.09904
Residual 0.178592 0.42260
Number of obs: 297, groups: Vowel, 26; Participant, 18
Fixed effects:
Estimate Std. Error df t value
(Intercept) -1.43762 0.07990 21.75516 -17.992
LanguageTamil 0.03926 0.09777 20.19149 0.402
Pr(>|t|)
(Intercept) 0.0000000000000151 ***
LanguageTamil 0.692
Signif. codes: 0 ‘*’ 0.001 ‘’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Correlation of Fixed Effects:
(Intr)
LanguageTml -0.667
I can see that Language is not a statistically significant predicting factor for Prolongations. But how do I interpret the estimate of 'LanguageTamil'(0.3926) when it is a categorical variable (French or Tamil) and there is no "1 unit increase" between the two. Does this actually mean that when the participant spoke in Tamil, they prolonged 0.03926ms longer than when they did in French (but not stat significant)? Also, what does the negative sign in the 'Correlation of Fixed Effects' mean? (-0.667).
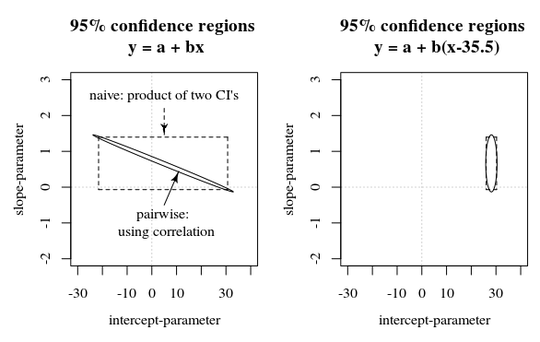
Duration. The ratio of geometric means is $\exp(0.03926) = 1.04$, meaning that Tamil speakers have an about 4% higher geometric mean ofDurationcompared to French speakers. – COOLSerdash Jun 24 '22 at 11:06