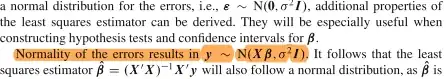Relationship between normally distributed errors (bivariate OLS regression) and bivariate normality of variables (Pearson’s r)

Question

I have forty quite diverse statistical text books at hand but I cannot find a reliable answer. I’ve studied the following and associated threads, but they didn’t got into it that deep: here and here. Here is also a related question that never got answered.

I am wondering whether one of the two assumptions is a special case of the other. My assumptions are (please correct me if I got it wrong).

1. In order to statistically infer the population correlation parameter rho from the sample’s point estimate Pearson’s r bivariate normal distribution of the two variables within the population is required (Bortz & Schuster (2010). Statistik, p. 162. Springer: Berlin). (I understand: in order to statistically test r for significance I first have to statistically test for bivariate normality).
2. Statistical tests on Beta (derived from a simple linear OLS regression) require normally distributed errors: “[talking about the OLS estimator...] In order to have exact tests and intervals, the assumption of normally distributed errors is needed” (Fahrmeir et al. (2013). Regression, p. 118. Springer: Heidelberg).
3. Pearson’s r = Beta (the standardized regression coefficient) for the simple linear regression (Fahrmeir et al. (2013). Regression, p. 113. Springer: Heidelberg).

4. Since the mathematical “=“ in Point 3) is to be understood as “exactly equal”, I infer that the same assumptions should apply for statistical testing of r and Beta in the bivariate case. Answer 3 in the first thread linked above supports this.
5. If it helps, on page 118 Fahrmeir also says the following, which I do not understand without translation:

I suspect, since OLS regression is more general than Pearson’s r, normally distributed errors are broader/more difficult to achieve and coincide with bivariate normally distributed variables for the bivariate case but I can't find a sensible reference.

So, my questions are:

1. Are the two assumptions mathematically related for the bivariate case and how?
2. Is there a way to communicate this non-mathematically?
3. In case one follows from the other, which one is more general, i.e. harder to achieve in practice?
4. Has anyone got a reliable reference?