0

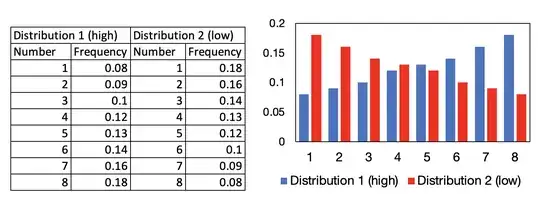
I am trying to find the answer for the following question. I have two distributions of numbers between 1 and 8, as illustrated here:

Distributuions

I draw random samples from each distribution, which we can call "bucket" here, with random length, and I need to predict which "bucket" form the two has the high distribution, based on both samples.

I have tried a few calculation methods, but I am not sure if they are correct. I will briefly mention them based on the sample examples (I prepared some obvious ones):

Sample from bucket 1: [2, 3, 5, 1, 1, 5, 2, 7, 6]

Sample from bucket 2: [6, 3, 5, 7, 8, 7, 4, 5, 6, 2, 5]

First, I tried a common bayesian rule, which gives me the probability over each sample (starting from a 50/50 prior), like, sample 1 (0.13 high, 0.87 low), sample 2 (0.85 high, 0.15 low). But that doesn't give me a probability over the buckets.

I have then tried several approaches, and I think the most accurate results came from the stress-strength method, suggested in this thread Probability that random variable B is greater than random variable A. Using this method and soving for P(sample 1 < sample 2) I get the following results: Z value of 0.60, which translates to 0.7257 when converted to standard distribution, therefore my results is:

P(sample 1 < sample 2) = 1 - 0.7257, which is a 23% chance that sample 1 comes from the "low" bucket.

I would like to know if this approach would be appropriate for this problem, and if not if there are any suggestions of methods I could use to solve this? Thank you very much in advance.

vferraz
  • 63
  • 2
    A standard powerful way to make such a comparison is to compute the ratio of the two likelihoods (each possible distribution determines a likelihood of the data). It is impossible to produce an answer of the form you request unless you adopt a prior distribution. But, again, all you have to do is update that by multiplying the prior odds by the likelihood ratio. This is Bayes' Theorem. – whuber Apr 29 '22 at 19:09
  • Thanks! But how would this give me information about "which bucket" to select as the high or low? The likelihood ratios from each sample (in the example above) are sample1: 0.1304, sample2: 0.1521. If I have a 0.5 prior, what would be the way to solve it with two likelihood ratios? – vferraz Apr 29 '22 at 19:15
  • 1
    Bayes' Theorem gives you the posterior distribution. Ordinarily you would choose the "bucket" with the highest posterior probability. – whuber Apr 29 '22 at 19:19

2 Answers2

4

I draw random samples from each distribution, which we can call "bucket" here, with random length, and I need to predict which "bucket" form the two has the high distribution, based on both samples.

I take that to mean that included in the prior information is that one of the buckets contains samples from low and the other contains samples from high.

starting from a 50/50 prior

I take that to mean that before any observations, bucket 1 is equally likely to be sampling from high as from low.

Here $HL$ indicates bucket 1 contains samples from high and bucket 2 contains samples from low, and $X$ is all 20 samples. Starting with Bayes' Theorem:

$$ P(HL|X)=\frac{P(X|HL)P(HL)}{P(X|HL)P(HL)+P(X|LH)P(LH)} $$ $P(X|HL)=0.9\cdot0.1\cdot0.13\cdot...\approx 6.40\cdot10^{-20}$

$P(X|LH)=0.16\cdot0.14\cdot0.12...\approx 6.23\cdot10^{-18}$

$P(LH)=P(HL)=0.5$

So,

$P(HL|X)\approx 0.019$

In R:

dfDist <- data.frame(X = 1:8,
                     PHigh = c(0.08, 0.09, 0.1, 0.12, 0.13, 0.14, 0.16, 0.18))
dfDist$PLow <- rev(dfDist$PHigh)
dfDist
#>   X PHigh PLow
#> 1 1  0.08 0.18
#> 2 2  0.09 0.16
#> 3 3  0.10 0.14
#> 4 4  0.12 0.13
#> 5 5  0.13 0.12
#> 6 6  0.14 0.10
#> 7 7  0.16 0.09
#> 8 8  0.18 0.08

Bucket1 <- c(2,3,5,1,1,5,2,7,6)
Bucket2 <- c(6,3,5,7,8,7,4,5,6,2,5)
P_HL <- 0.5


(P_X_HL <- prod(c(dfDist$PHigh[Bucket1], dfDist$PLow[Bucket2])))
#> [1] 6.398966e-20
(P_X_LH <- prod(c(dfDist$PLow[Bucket1], dfDist$PHigh[Bucket2])))
#> [1] 3.225079e-18
(P_HL_X <- P_X_HLP_HL/(P_X_HLP_HL + P_X_LH*(1 - P_HL)))
#> [1] 0.01945525
jblood94
  • 1,459
  • Thank you for the suggestion, I am gonna try it out right now! So based on these numbers it would be correct to affirm bucket 1 has a 1.9% probability of coming from the high, while bucket 2 has a 98.1% probability of coming from the high, is this correct? I – vferraz May 03 '22 at 11:18
  • Yes, that is correct. – jblood94 May 03 '22 at 11:25
2

First, I tried a common bayesian rule, which gives me the probability over each sample (starting from a 50/50 prior), like, sample 1 (0.13 high, 0.87 low), sample 2 (0.85 high, 0.15 low). But that doesn't give me a probability over the buckets

It gives you a probability over the distributions high and low.

Bucket 1 has 13% probability to be from distribution high and 87% to be from distribution low.

Bucket 2 has 85% probability to be from distribution high and 15% to be from distribution low.

Or possibly you want to compare the two following models:

  • model 1: bucket one is from distribution one and bucket two is from distribution two

versus

  • model 2: bucket one is from distribution two and bucket two is from distribution one

You can model this in a similar fashion by computing the likelihood ratio for both models.

Sextus Empiricus
  • 77,915