Predictive parametric models and their (unknowable?) coefficients signs

Question

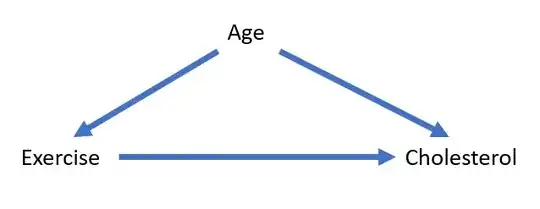
Suppose the DAG below is the true, complete, DAG for the effect of $Exercise$ on $Cholesterol$. $Exercise$ lowers $Cholesterol$; $Age$ causes people to $Exercise$ more; $Age$ causes $Cholesterol$ to increase. Now suppose that we are not interested in causal effects; we are, instead, building a predictive model of $Cholesterol$ and we do not have access to the $Age$ variable/any proxies of the $Age$ variable/any variables that are ancestors of $Age$.

Without $Age$ in the picture, we notice that $Exercise$ and $Cholesterol$ are positively correlated. This strikes us as counterintuitive because we know that $Exercise$ decreases $Cholesterol$; if we had $Age$ to control for, we'd see that for each $Age$ group $Exercise$ and $Cholesterol$ are negatively correlated.

Given the setup (we do not have access to $Age$/any proxies of $Age$/any variables that are ancestors of $Age$), if I am not mistaken, no matter what predictors we include in a predictive model of $Cholesterol$, the coefficient on $Exercise$ will always be positive (which doesn't make sense to us given our knowledge of the direct causal effect of $Exercise$ on $Cholesterol$).

Is there any sense in which because of the counter-intuitive sign on $Exercise$, a predictive model that includes $Exercise$ is flawed or we'd care less about estimating that coefficient with precision? Now let's throw away the confines of this contrived example: In the real world, can we have any reasonable expectation about what the signs of the predictors in a parametric predictive model would be?

Credits: In this post, I have repurposed an excellent example from Judea Pearl' book "Causal Inference in Statistics".

Answer 1

Your first question: "Is there any sense in which because of the counter-intuitive sign on Exercise, a predictive model that includes Exercise is flawed or we'd care less about estimating that coefficient with precision?"

Your example of Simpson's paradox from Pearl's book shows, that correlation must not be confused with causal effects. Because of the hidden confounder Age, you can have a positive correlation but a negative causal effect. But that doesn't mean that the positive correlation would be somehow wrong or "flawed". Exercise and Cholesterol do have positive correlation and this fact can and should be used when predicting Cholesterol only from Exercise.

Your second question: "In the real world, can we have any reasonable expectation about what the signs of the predictors in a parametric predictive model would be?"

The "signs of predictors" in models can be "trusted", as long as we interpret them stochastically and not causally. This is true in the real world as in the given example.

But maybe your question should be understood as: "How much can we learn about causal relationships from purely observational (stochastic) data?". E.g., how do we know that there are not always hidden confounders, like Age in the example, that turn negative causal effects into positive correlations? Those are questions that the field of "causal discovery" is concerned with. This is a huge research discipline, and it is difficult to give short answers. But it is fair to say that, in general, it is very difficult, and often impossible, to infer the true causal relations, especially if the presence of hidden confounders cannot be ruled out. And in practice, you almost never can.

Having said that, there are many methods that can be tried, often presuming certain constraints, like e.g. linearity or additive noise, and frequently relying on interventional data. And some of them can even deal with hidden confounders, and even with cyclic structures, see e.g. here or here.