how to interpret the interaction term in lm formula in R?

Question

In R, if I call the lm() function in the following way:

lm.1 = lm(response ~ var1 + var2 + var1 * var2)
summary(lm.1)

This gives me a linear model of the response variable with var1, var2 and the interaction between them. However, how exactly do we numerically interpret the interaction term?

The documentation says this is the "cross" between var1 and var2, but it didn't give an explanation of what exactly the "cross" is.

It would be helpful for me to know what exact numbers R is calculating to incorporate the interaction between the two variables.

Answer 1

The standard way to write the prediction equation for your model is:

$\hat y = b_0 + b_1*x_1 + b_2*x_2 + b_{12} * x_1 *x_2$

But understanding the interaction is a little easier if we factor this differently:

$\hat y = (b_0 + b_2*x_2) + (b_1 + b_{12}*x_2) * x_1$

With this factoring we can see that for a given value of $x_2$ the y-intercept for $x_1$ is $b_0 + b_2*x_2$ and the slope on $x_1$ is $(b_1 + b_{12}*x_2)$. So the relationship between $y$ and $x_1$ depends on $x_2$.

Another way to understand this is by plotting the predicted lines between $y$ and $x_1$ for different values of $x_2$ (or the other way around). The Predict.Plot and TkPredict functions in the TeachingDemos package for R were designed to help with these types of plots.

Answer 2

It is easiest to think about interactions in terms of discrete variables. Perhaps you might have studied two-way ANOVAs, where we have two grouping variables (e.g. gender and age category, with three levels for age) and are looking at how they pertain to some continuous measure (our dependent variable, e.g. IQ).

The x1 * x2 term, if significant, can be understood (in this trivial, made-up example) as IQ behaving differently across the levels of age for the different genders. For example, maybe IQ is stable for males across the three age groups, but young females start below young males and have an upward trajectory (with the old age group having a higher mean than the old age group for males). In a means plot, this would imply a horizontal line for males in the middle of the graph, and perhaps a 45 degree line for females that starts below males but ends above males.

The gist is that as you move along the levels of one variable (or "holding X1 constant"), what is going on in the other variable changes. This interpretation also works with continuous predictor variables, but is not so easy to illustrate concretely. In that case, you might want to take particular values of X1 and X2 and see what happens to Y.

Answer 3

Suppose you get point estimates of 4 for $x_1$, 2 for $x_2$ and 1.5 for the interaction. Then, the equation is saying that the lm fit is

$y = 4x_1 + 2x_2 + 1.5x_1x_2$

Is that what you wanted?

Answer 4

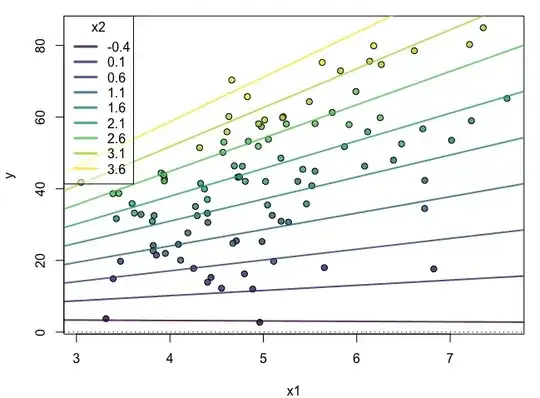
Based on @Greg Snow's answer, I just wanted to add a simulation showing this:

set.seed(6);library(viridis)
n = 100
x.lm1 = rnorm(n = n, mean = 5, sd = 1)
x.lm2 = rnorm(n = n, mean = 2, sd = 1) # Note that this doesn't have to be normally distributed. This could be a uniform distribution or from a binomial.
beta0 = 2.5
beta1 = 1.5
beta2 = 2
beta3 = 3
err.lm = rnorm(n = n, mean = 0, sd = 1)
y.lm = beta0 + beta1*x.lm1 + beta2*x.lm2 + beta3*x.lm1*x.lm2 + err.lm
df.lm = data.frame(x1 = x.lm1, x2 = x.lm2, y = y.lm)
lm.out = lm(y~x1*x2, data = df.lm)
Make a new range of x2 values on which we will test the effect of x1
x2r = range(x.lm2)
x2.sim = seq(x2r[1],x2r[2], by = .5)
this is the effect of x1 at different values of x2 (which moderates the effect of x1)
eff.x1 <- coef(lm.out)["x1"] + coef(lm.out)["x1:x2"] * x2.sim # this gets you the slopes

eff.x1.int <- coef(lm.out)["(Intercept)"] + coef(lm.out)["x2"] * x2.sim # this gets you the intercepts

eff.dat <- data.frame(x2.sim, eff.x1, eff.x1.int)
virPal <- viridis::viridis(length(x2.sim),alpha = .8)
eff.dat$x2.col <- virPal[as.numeric(cut(eff.dat$x2.sim,breaks = length(x2.sim)))]
df.lm$x2.col <- virPal[as.numeric(cut(df.lm$x2,breaks = length(x2.sim)))]
par(mfrow=c(1,1), mar =c(4,4,1,1))
plot(x = df.lm$x1, y = df.lm$y, bg = df.lm$x2.col, 
     pch = 21, xlab = "x1", ylab = "y")
apply(eff.dat, 1, function(x) abline(a = x[3], b = x[2], col = x[4], lwd  = 2))
abline(h = 0, v = 0,lty = 3)
legend("topleft", title = "x2",legend = round(eff.dat$x2.sim,1), lty = 1, lwd = 3,
       col = eff.dat$x2.col, bg = scales::alpha("white",.5))