3

Say we have a random variable $$ X = A_0 A_1 + A_0 A_2 + A_1 A_2, $$ which consists of normally distributed independent random variables $A_0, A_1, A_2 \sim \mathcal{N}(0,1)$ with probability density function (PDF) $$ f_{A_i}(x) = \frac{1}{\sqrt{2 \pi}} e^{-\frac{x^2}{2}} . $$ How do I derive the PDF of $X$ ?
So far I have been able to express the PDF of $Y = A_i A_j$ for $i \neq j$ which yields $$ f_Y(y) = \frac{1}{\pi \sigma_{i} \sigma_{j}} K_0\Big(\frac{|y|}{\sigma_{i} \sigma_{j}} \Big) = \frac{1}{\pi} K_0\Big(|y| \Big), $$ where $K_0(.)$ is the second kind modified Bessel function. I also tried to factorize $X$ into $$ X = A_0 (A_1 + A_2) + A_1 A_2 = Y_0 + Y_1, $$ where there is a sum of two Bessel distributions $Y_0$ and $Y_1$, however, I learned that I cannot just use convolution of their marginal PDFs due to their correlation.
I have done some simulations in MATLAB and obtained the following graphs of PDF and CDF:

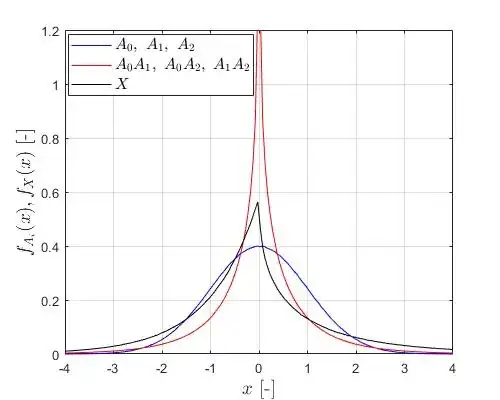
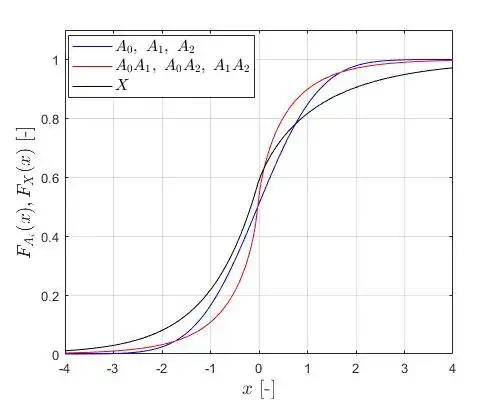
Basically, I am looking for a mathematical representation of the black curve in the above PDF graph. I cannot help myself but it seems very counter-intuitive that $X$ has a nonsymmetric PDF.
I think that first I have to obtain the joint probability density function $f_{Y_0, Y_1}(y_0, y_1)$ so I can use it in $$ f_{X}(x) = \int f_{Y_0, Y_1}\big(s, x-s \big)\ ds, $$ but I dont know how to get $f_{Y_0, Y_1}(y_0, y_1)$. In similar threads I saw people mentioning copula but I cannot see how it helps me in my situation...
Is there any area of mathematics that deals with this sort of problems ?

Radim Zedka
  • 31
  • 2
  • 4
    This is a quadratic form and therefore can be diagonalized. Because it is not positive-definite, the result will be a difference of multiples of chi-squared distributions. You can compute it using characteristic functions (or mgfs), following the methods at https://stats.stackexchange.com/a/72486/919 (chi-squared distributions are Gamma). The solution is given at https://stats.stackexchange.com/questions/478495. – whuber Mar 10 '22 at 21:24
  • Re intuition about asymmetry: at first blush that is a surprise. But what would it take to negate $X$? You can't accomplish that with any of the obvious symmetries of the $A_i:$ permuting them won't alter $X$ and negating any subset of them does not negate $X.$ The symmetries of $X$ can be found by diagonalizing its associated symmetric matrix: the direction $(1,1,1)$ is special and otherwise the form is rotationally invariant around that axis, giving eigenspaces of dimensions $1$ and $2,$ resp. Thus the distribution of $X$ is the difference of chi-squared distributions with different df. – whuber Mar 10 '22 at 23:34
  • Thank you very much, whuber, for your guidance ! After studying your links I came across https://math.stackexchange.com/questions/3700360 where they discuss the exact problem. – Radim Zedka Mar 11 '22 at 20:52

0 Answers0