Visualizing multivariate multiple regression of continuous data in R

Question

I have created a multivariate multiple regression model with 3 dependent and 3 independent variables in R, and would like to generate meaningful visualizations. All variables are continuous. When working with multiple regression models with 1 dependent variable, this is fairly easy.

For example

set.seed(0)
df <- data.frame(ind1 = c(1:10),
                ind2 = runif(10,5,15),
                ind3 = runif(10,5,15))
df$dep1 <- df$ind1 * df$ind2 * df$ind3
df$dep2 <- df$ind1 * df$ind2 * df$ind3 * runif(10)
df$dep3 <- df$ind1 * df$ind2 * df$ind3 * abs(rnorm(10))
model1 <- lm(data = df, dep1 ~ ind1 + ind2 + ind3)

There are simple options for different insightful visualizations

library('ggplot2')
library('ggeffects')
ggplot(ggpredict(model1, terms = c("ind1 [1,5,10]", "ind2", "ind3")), 
       aes(x, predicted, color = group)) + geom_line() + facet_wrap(~facet)

library('car')
avPlots(model1)

library('sjPlot')
plot_model(model1, type = 'diag')

However, in a model with 3 dependent variables

model2 <- lm(data = df, cbind(dep1, dep2, dep3) ~ ind1 + ind2 + ind3)

these options seem to go out the window. I am hoping to come up with something a little more powerful than simply

hist(resid(model2))

Let me know if this topic is a better fit for R StackOverflow.

Answer 1

I think you might do best to review multivariate regression (meaning no disrespect). There is a short tutorial at UVA's stats help page here: https://data.library.virginia.edu/getting-started-with-multivariate-multiple-regression/. They explain that multivariate regression is mostly the same as several univariate regressions, except that there are covariances between the betas for the different outcomes that need to be taken into account when testing the variables. In particular, they mention that the relevant plots are the same:

The same diagnostics we check for models with one predictor should be checked for these as well.

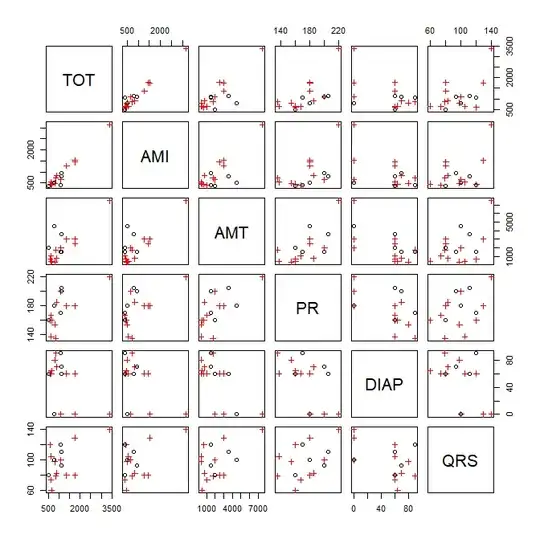
I will use their example to illustrate some data visualizations below (coded in R). I'll start with a scatterplot matrix of the data. GEN is binary, so I'll represent that with a different color and symbol. After fitting the model, if you try to run plot.lm() you'll get an error. However, it's easy enough to reproduce those plots manually. To plot a multiple regression model without interactions, you can pick a variable of interest and make a scatterplot with it and the response and draw the fitted function over it. Be sure to adjust the intercept by setting other variables at their means (see my answer to How to visualize a fitted multiple regression model?). You can also make scatterplots and qq-plots of the residuals (the latter lets you assess if their distribution is similar).

ami_data = read.table("http://static.lib.virginia.edu/statlab/materials/data/ami_data.DAT")
names(ami_data) = c("TOT","AMI","GEN","AMT","PR","DIAP","QRS")

summary(ami_data)
# output omitted
pairs(ami_data[,-3], col=ifelse(ami_data$GEN, "red", "black"),
                     pch=ifelse(ami_data$GEN, 3, 1))

mlm1 = lm(cbind(TOT, AMI) ~ GEN + AMT + PR + DIAP + QRS, data=ami_data)
summary(mlm1)
# output omitted
head(resid(mlm1))
#          TOT        AMI
# 1  132.82172  161.52769
# 2  -72.00392 -264.35329
# 3 -399.24769 -373.85244
# 4 -382.84730 -247.29456
# 5 -152.39129   15.78777
# 6  366.78644  217.13206
windows()
  plot(mlm1)
# Error: 'plot.mlm' is not implemented yet
reproducing R's plot.lm() for TOT
rst = rstandard(mlm1)  # standardized residuals
windows()

  layout(matrix(1:4, nrow=2, byrow=T))
plot 1
plot(resid(mlm1)[,1]~fitted(mlm1)[,1], 
       main="Residuals vs Fitted for TOT", xlab="fitted", ylab="residuals")
  lines(lowess(resid(mlm1)[,1]~fitted(mlm1)[,1]), col="red")
plot 2
plot(sqrt(abs(rst[,1]))~fitted(mlm1)[,1], 
       main="Scale-Location plot for TOT", xlab="fitted", ylab="residuals")
  lines(lowess(sqrt(abs(rst[,1]))~fitted(mlm1)[,1]), col="red")
plot 3
qqnorm(rst[,1], main="qq-plot of residuals TOT")
  qqline(rst[,1])
plot 5
plot(rst[,1]~lm.influence(mlm1)$hat, xlab="Leverage", ylab="residuals",
       main="Residuals vs Leverage for TOT")
  lines(lowess(rst[,1]~lm.influence(mlm1)$hat), col="red")

windows()  
  layout(matrix(1:4, nrow=2, byrow=T))
  # plot of model for TOT vs AMT
  plot(TOT~AMT, ami_data, main="TOT vs AMT w/ data & model", 
       col=ifelse(ami_data$GEN, 2, 1), pch=ifelse(ami_data$GEN, 3, 1))
  abline(coef(mlm1)[-3,1]%*%c(1, apply(ami_data[,c(3,5:7)], 2, mean)),
         coef(mlm1)[3,1], col="blue")
  # plot of model for AMI vs AMT
  plot(AMI~AMT, ami_data, main="AMI vs AMT w/ data & model", 
       col=ifelse(ami_data$GEN, 2, 1), pch=ifelse(ami_data$GEN, 3, 1))
  abline(coef(mlm1)[-3,2]%*%c(1, apply(ami_data[,c(3,5:7)], 2, mean)),
         coef(mlm1)[3,2], col="blue")
  # scatterplot of residuals
  plot(resid(mlm1)[,1], resid(mlm1)[,2], xlab="Residuals for TOT",
       ylab="Residuals for AMI", main="scatterplot of residuals")
  # qq-plot of residuals
  qqplot(resid(mlm1)[,1], resid(mlm1)[,2], xlab="Residuals for TOT",
         ylab="Residuals for AMI", main="qq-plot for residuals")

Answer 2

One option is to create a 3D surface plot showing the sensitivity of your dependent variables to the independent variables in your model.

First, create sequences (length = 10 here) along your independent variables.

df2 <- data.frame(ind1 = seq(from = min(df$ind1), to = max(df$ind1), by = (max(df$ind1)-min(df$ind1))/9),
                  ind2 = seq(from = min(df$ind2), to = max(df$ind2), by = (max(df$ind2)-min(df$ind2))/9),
                  ind3 = seq(from = min(df$ind3), to = max(df$ind3), by = (max(df$ind3)-min(df$ind3))/9))

Next, generate a series of predictions.

tst <- predict(model2, df2)

Now, you can plot these predicted values of dep1,dep2,anddep3 as a 3D surface.

library('plotly')
generate a numeric matrix for use with plotly::plot_ly
mat <- matrix(ncol = ncol(tst), nrow = nrow(tst))
populate matrix with numeric values from model prediction
for (i in 1:3) {
  mat[,i] <- tst[,i]
}
generate 3D surface
plot_ly(type = 'surface', z = mat) %>%
customize axis titles
layout(scene = list(xaxis = list(title = 'dep1'),
                      yaxis = list(title = 'dep2'),
                      zaxis = list(title = 'dep3')))

This creates an interactive plot. A still image is shown here

Answer 3

Hypothesis tests in multivariate multiple regression models can be visualized using hypothesis-error (HE) plots, implemented in the heplots package, https:friendly.github.io/heplots/

These show data ellipses for the residuals (E) in relation to the predictors (H). For 1 df regression terms, the H "ellipses" collapse to a line. They have the property that the H ellipse projects outside the E ellipse if and only if the term is significant by Roy's test.

For this example, we get:

library(heplots)
heplot(model2, fill=TRUE, fill.alpha=0.1)

Here, only ind1 is significant.

> car::Anova(model2, test="Roy")
Type II MANOVA Tests: Roy test statistic
     Df test stat approx F num Df den Df Pr(>F)

ind1  1      6.14     8.19      3      4  0.035 *
ind2  1      1.43     1.91      3      4  0.270

ind3  1      1.45     1.94      3      4  0.265

Signif. codes:  0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1

A scatterplot matrix version is obtained using pairs.mlm

pairs(model2, , fill=TRUE, fill.alpha=0.1)

The angles of the H lines for the predictors ind1, ind2, and ind3 wrt the dep variables show the correlations of the former with the latter.

For more complex models, involving factors (df > 1 terms), these results can be visualized in "canonical space" using the candisc package, candisc