0

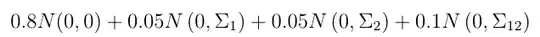
How can I generate a random variable which follows the mixture Gaussian distributions: enter image description here

I found the answer and tried to simulate it, but I think it is not the right dataset I wanted.

Here is my code:

M = 100
sigma1 = matrix(c(0.2, 0, 0, 0),ncol=2)
sigma2 = matrix(c(0, 0, 0, 0.4),ncol=2)
sigma12 = matrix(c(0.2, 0.028, 0.028, 0.4),ncol=2)
U = runif(M)
b = cbind(rep(NA,M),rep(NA,M))
for (i in 1:M) {
  if (U[i]<.8) {
    b[i,] = c(0,0)
  } else if (U[i]<.85) {
    b[i,] = rmvnorm(1,sigma = sigma1)
  } else if (U[i]<.9) {
    b[i,] = rmvnorm(1,sigma = sigma2)
  } else {
    b[i,] = rmvnorm(1,sigma = sigma12)
  }
}

Is there something wrong? Thanks in advance!

lele
  • 23
  • Why do you assume it's wrong? – Tim Feb 11 '22 at 06:53
  • Are you sure you want a Gaussian with zero variance? Also, you use undefined variables in the code (genMat1, ...) – frank Feb 11 '22 at 07:22
  • @frank, sorry, I've fixed the typo in the code (sigma1 instead of genMat1). And yes, I want a Gaussian with zero variance. – lele Feb 11 '22 at 13:25
  • 1
    There is no Gaussian with zero variance. You probably want a singular probability mass at zero? – frank Feb 11 '22 at 13:39
  • The simulated data looks good to me. So, I would repeat @Tim's question: why do you assume it is wrong? – frank Feb 11 '22 at 13:47
  • I plot the true density as a sanity check shown in the answer(link) x = seq(-20,20,.1) truth = .8*cbind(rep(0,nrow(x)),rep(0,nrow(x)))+.05*dmvnorm(x,sigma = sigma1) + .05*dmvnorm(x,sigma = sigma1) + .1*dmvnorm(x,sigma =sigma12) plot(density(d),main="Density Estimate of the Mixture Model",ylim=c(0,.2),lwd=2) lines(x,truth,col="red",lwd=2) The truth density plot is different from b density. – lele Feb 11 '22 at 14:30

0 Answers0