1

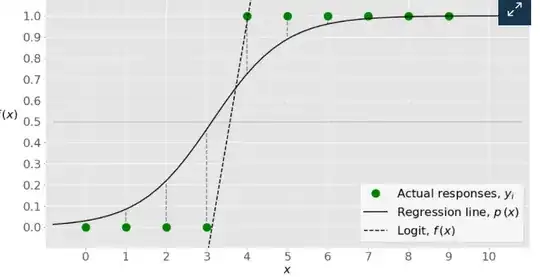
let's assume we have continuous independent variable and obviously binary dependent one. How can we calculate probabilities which is displayed on y-axis? With scale like in the image below, it's clear that we can simply take some x value, look through all the samples having this value and corresponding y values and calculate a/(a+b). But, how do I find probabilities if I have continuous variable?

Sigmoid function

ilyalipnitsky
  • 61
  • 5
    Please clarify what kind of answer you need: are you asking how to perform logistic regression? How to perform an exploratory smooth of the data? How to convert the log odds as estimated by logistic regression into probabilities? About the formula for logistic regression? Something else, perhaps? – whuber Feb 02 '22 at 19:55
  • How to find probabilites as displayed on y-axis – ilyalipnitsky Feb 02 '22 at 20:04
  • 2
    The y-axis is already displayed in probabilities - you just read off the regression line...unless I am missing something in your question? – André.B Feb 02 '22 at 20:12
  • I would also, normally, expect to see some variance around your points (hopefully binomial), which would make the fitted line look more reasonable. – André.B Feb 02 '22 at 20:13
  • 2
    @ilyalipnitsky the answer is "by using logistic regression" as the figure shows results of logistic regression, so could you be more precise on what exactly is unclear for you? – Tim Feb 02 '22 at 20:18
  • Sorry for being unclear. I mean how to calculate probabilities of points which displayed by light gray lines (e.g. with x = 2, p = 0.2). – ilyalipnitsky Feb 02 '22 at 20:19
  • I would appreciate if you cite exact formula. Thanks. – ilyalipnitsky Feb 02 '22 at 20:21
  • See https://stats.stackexchange.com/a/69873/919 for the formula, illustrations, and working code. If your question is about reading this graph, see https://stats.stackexchange.com/a/314363/919. – whuber Feb 02 '22 at 20:43

1 Answers1

3

You calculate the linear part of the generalized linear model.

$$ \beta_0+\beta_1x_i $$

Then you transform the linear part according to the inverse link function. $$\beta_0+\beta_1x_i = \log\bigg(\dfrac{p_i}{1-p_i}\bigg)\implies p_i =\dfrac{ 1 }{ 1+\exp(-(\beta_0+\beta_1x_i)) } $$

Community
  • 1
Dave
  • 62,186
  • Your notation is potentially confusing because "$y_i$" refers to "Actual responses" in the question, whereas your $y_i$ appears to refer to a hypothesized log odds. At the very least, please explain in words the meanings of your $y_i$ and $p_i$ and describe their corresponding elements in the OP's graphic. – whuber Feb 02 '22 at 20:30