Why points above the line is labeled as positive and below as negative?
In short, because above/below that line is the space where the model would predict positive/negative classes.
What you've likely plotted is the decision boundary for the learned model. The colors correspond to the predictions the model would make rather than the actual classes.
In classification problems, it is common to assign the positive class to points where the predicted probability is greater than 0.5. The decision boundary is the set of points $(x_1, x_2)$ where
$$ D(x_1, x_2) =\hat{\beta}_0 + \hat{\beta}_1x_1 + \hat{\beta}_2x_2 = 0 $$
Note that the $D(x_1, x_2)$ operates on the log odds scale. Hence, we assign the positive class to points where $D(x_1, x_2)>0$.
We can create our own version of your picture in R, and demonstrate this. Note that colors correspond to predicted class membership while shapes correspond to actual class membership. The decision boundary is not plotted explicitly but you can see where it might be implicitly. Note that there are different shapes in each color, indicating that the model makes some classification errors in the training set.
library(tidyverse)
n = 500
x1 = runif(n)
x2 = runif(n)
eta = 0.125 + x1 - x2
p = plogis(eta)
y = rbinom(n, 1, p)
d = tibble(x1, x2, y)
model = glm(y~., data = d, family = binomial())
d$est_p = predict(model, type='response')
d$ypred = as.numeric(d$est_p>0.5)
d %>%
ggplot(aes(x1, x2, color=factor(ypred), shape=factor(y)))+
geom_point()+
theme(aspect.ratio = 1)

Why we write value of y as (w^t * x) / ||w||, where (w^t * x) / ||w|| is the distance between the point and the line?
We don't write $y=w^T\mathbf{x}$, but the decision boundary can be written as a linear combination of the features. It it is common to consider a row of a design matrix to have an additional 1 appended to the start of the vector. This means $\mathbf{x} = (1, x_1, x_2)$. If we consider $w = (\beta_0 , \beta_1 , \beta_2)$ then $D(x_1, x_2) = w^T \mathbf{x}$. This means the positive class would be assigned when $w^T\mathbf{x}>0$. I'm not sure where you've seen these equations, but I don't typically see $w$ written as a unit vector.
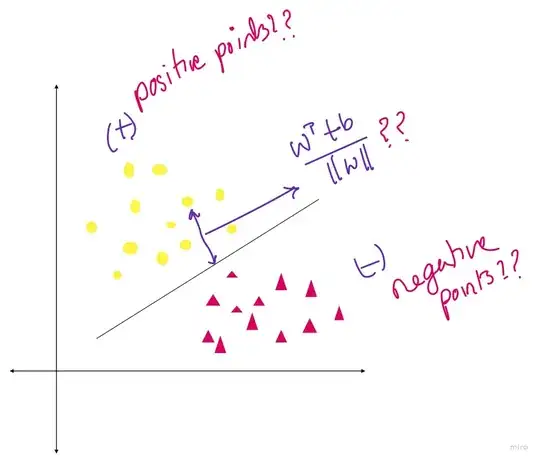 I have two primary questions on logistic regression from a geometric point of view.
I have two primary questions on logistic regression from a geometric point of view.