Goodness of Fit for (presumably) poisson distributed data

Question

I have some counting data which lists numbers of some incidence in 10 minute intervals. obs=[1125,1117,1056,...1076] observations in some 112 time intervals.

The data is supposedly Poisson distributed - expecting to see around 1000 incidences in any 10 minutes - but when I try to perform a goodness-of-fit test, I get a p-value of 0.0 --- Now sometimes you simply have to reject your null hypothesis, but I can't help but shake the feeling that I'm doing something wrong, as it's been a while since I had any training in hypothesis testing. The data itself is shown below (with an MLE Poisson pmf plotted on top).

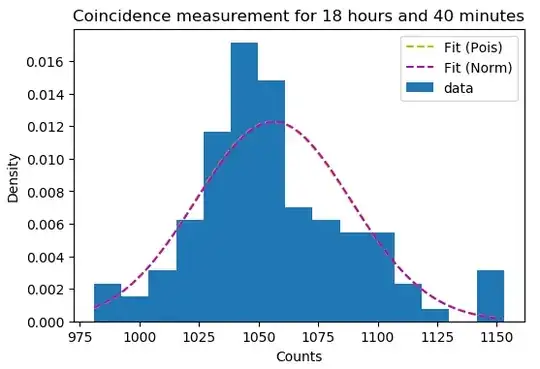
The rate parameter $\lambda$ is estimated with an MLE $\lambda=\overline{n}$, that is; it's just the mean of observations.

I'm using Python and scipy.stats to perform the GoF-test;

from scipy.stats import poisson
from scipy.stats import chisquare
from scipy.stats import chi2
MLE = np.mean(obs)
#H0: The data is Poisson distributed with rate lambda=MLE
#H1: The data is not Poisson distribtued
#under the null hypothesis, the expected values for x observations
with x = 981, 982,..., 1153           (min and max of observations)
Probs = poisson.pmf(obs,MLE)
Ex = Probs * sum(obs)
chisq = sum(((obs-Ex)**2)/Ex)    #this tallies up to 253978.198
categories         params   constant
df=(len(np.unique(coinc)))   - 1     - 1
#Chi-squared statistic
chi2.pdf(chisq,df)     #this is 0.0
#"automatic version"
chisquare(obs,Ex,df)   #returns p-value 0.0

I feel as though I'm messing up by not dividing the data into "categories" in some fashion - as some of the intervals actually do have the same number of counts, for instance the value 1054 occurs three times in the list. Arranging the data into a histogram, however, leaves me a little uncertain how to calculate the expected values (under the null hypothesis).

Edit: Here's the actual data, for testing:

obs = [1125, 1117, 1056, 1069, 1060, 1009, 1065, 1031, 1082, 1034,  985,
       1022, 1020, 1108, 1084, 1049, 1032, 1064, 1036, 1034, 1046, 1086,
       1098, 1054, 1032, 1101, 1044, 1035, 1018, 1107, 1039, 1038, 1045,
       1063,  989, 1038, 1038, 1048, 1040, 1050, 1046, 1073, 1025, 1094,
       1007, 1090, 1100, 1051, 1086, 1051, 1106, 1069, 1044, 1003, 1075,
       1061, 1094, 1052,  981, 1022, 1042, 1057, 1028, 1023, 1046, 1009,
       1097, 1081, 1147, 1045, 1043, 1052, 1065, 1068, 1153, 1056, 1145,
       1073, 1042, 1081, 1046, 1042, 1048, 1114, 1102, 1092, 1006, 1056,
       1039, 1036, 1039, 1041, 1027, 1042, 1057, 1052, 1058, 1071, 1029,
        994, 1025, 1051, 1095, 1072, 1054, 1054, 1029, 1026, 1061, 1153,
       1046, 1076]

EDIT: Given the comments, I've tried to redo this with histogram'ing instead. However, I run into a problem with the expectation value for each histogram bin (incidentally, I'm not certain I did it right. Not sure if I should take this question to stackexchange by now...), as some of them are always very low (<1). Generally $\Chi^2$ fits won't work with expectation values below 5 or so; so should I merge the bins before trying to calculate chisq?

# We first arrange data into a histogram
hist,bins,patches=plt.hist(obs,bins=10)
#We need to know which elements went into each bin
#np.digitize returns an array of indices corresponding to which bin from
bins that each value in obs belongs to.
E.g. the first entry is 5; meaning that first entry in obs belongs to
bin number 5
bin_indices=np.digitize(obs,bins)
#under the null hypothesis, the expected values for x observations
Ex=[]
for i in range(len(bins)):
    j=np.where(bin_indices==i)[0]
    #returns the indices of obs.data which goes in bin number i
    data_in_bin=coinc[j]
    #returns the coincidence data in that bin, e.g. obs[0] is in bin 5.
    if data_in_bin.size >0:
        Ex.append(poisson.pmf(data_in_bin,MLE).sum() * sum(hist))
chisq = sum(((hist-Ex)**2)/Ex)    #this tallies up to 128.60
categories    params   constant
df=(len(bins)-1)   - 1     - 1
#Chi-squared statistic
p=chi2.pdf(chisq,df)     #this is 1.21 e-55
print(p)
#"automatic version"
chisquare(hist,Ex,df)   #returns p-value 2.61 e-62

At least some progress was made though. We've gone from $p=0.0$ to $p=1.22\times10^{-55}$.

Answer 1

So I think the Chi-square approach works OK for low mean Poisson data, since setting the bins at integer values is the logical choice. With higher means though, it becomes more tricky -- you will get different answers with different binning strategies. Hence my suggestion for the KS test in the comments -- you don't need to bin the data at all, just look at the CDF.

But Glen_b is right, in that the KS test without prespecifying the mean will have too high of Type II error (false negatives). An alternative is the Lilliefors test, which uses the same CDF approach as the KS test, but uses simulations to generate the null distribution for the KS statistic.

First though, lets look at the CDF of your data. I thought your histogram looked pretty consistent with Poisson data, and the CDF graph comports with that as well. Here I generate 10 simulations of 112 observations to show the typical variation with data that is actually Poisson (with the same mean as your data):

from datetime import datetime
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.stats import poisson
obs = np.array([1125, 1117, 1056, 1069, 1060, 1009, 1065, 1031, 1082, 1034,  985,
       1022, 1020, 1108, 1084, 1049, 1032, 1064, 1036, 1034, 1046, 1086,
       1098, 1054, 1032, 1101, 1044, 1035, 1018, 1107, 1039, 1038, 1045,
       1063,  989, 1038, 1038, 1048, 1040, 1050, 1046, 1073, 1025, 1094,
       1007, 1090, 1100, 1051, 1086, 1051, 1106, 1069, 1044, 1003, 1075,
       1061, 1094, 1052,  981, 1022, 1042, 1057, 1028, 1023, 1046, 1009,
       1097, 1081, 1147, 1045, 1043, 1052, 1065, 1068, 1153, 1056, 1145,
       1073, 1042, 1081, 1046, 1042, 1048, 1114, 1102, 1092, 1006, 1056,
       1039, 1036, 1039, 1041, 1027, 1042, 1057, 1052, 1058, 1071, 1029,
        994, 1025, 1051, 1095, 1072, 1054, 1054, 1029, 1026, 1061, 1153,
       1046, 1076])
Simple ecdf function
def ecdf(x):
    sx = np.sort(x)
    n = sx.size
    sy = np.arange(1,n+1)/n
    return sx,sy
fig, ax = plt.subplots(figsize=(6,4))
CDF for observed data
ecdf_x,ecdf_y = ecdf(obs)
ax.step(ecdf_x,ecdf_y,color='red',label='ECDF',
        linewidth=3,zorder=3)
CDF for hypothetical poisson
pcdf_x = np.arange(obs.min(),obs.max()+1)
pcdf_y = 1 - poisson.cdf(obs.mean(),pcdf_x)
ax.step(pcdf_x,pcdf_y, color='k',linewidth=3,
        label=f'Poisson {obs.mean():.1f}',zorder=2)
Random variates of same size as obs
for i in range(10):
    randp = poisson.rvs(obs.mean(),size=len(obs))
    rcdf_x,rcdf_y = ecdf(randp)
    if i == 0:
        ax.step(rcdf_x,rcdf_y, color='grey',
                label=f'Simulated Poisson',zorder=1)
    else:
        ax.step(rcdf_x,rcdf_y, color='grey',alpha=0.35,zorder=3)
ax.legend(loc='upper left')
plt.show()

So you can see your data does not look like all that out of line with a Poisson process. Here I coded up a Lilliefor's version for Poisson (if you have the original timestamps, you could estimate an exponential distribution and check with Lilliefor's or statsmodels simulated lookup tables).

def lill_poisson(x,sim=10000,seed=10):
    n = len(x)
    nu = np.arange(1.0,n+1)/n
    nm = np.arange(0.0,n)/n
    # Fit parameters
    m = x.mean()
    fp = poisson(m) # frozen Poisson
    # in function for KS stat
    def ks(obs):
        x = np.sort(obs)
        cv = fp.cdf(x)
        Dp = (nu - cv).max()
        Dm = (cv - nm).max()
        return np.max([Dp,Dm])
    # KS stat observed
    ks_obs = ks(x)
    # Generate simulation
    np.random.seed(seed)
    sa = np.zeros(sim)
    for i in range(sim):
        s = fp.rvs(n)
        sa[i] = ks(s)
    # calculate p-value
    p_val = np.append(sa,ks_obs).argsort()[-1]/sim
    return ks_obs, p_val, sa
kstat, pval, svals = lill_poisson(obs)
print(f'KS Stat: {kstat:0.2f}, p-value {pval:0.2f}')

Your p-value may be slightly different due to the simulation run, but I don't think it is likely to be anything nearby the edge of the distribution.

To check and make sure my lill_poisson had close to the right uniform null distribution, I simulated Poisson data with varying means and sample sizes. It looks decent for critical values of 0.05 and 0.10, but the closer to the tail you get it doesn't work as well. That may be due to smaller sample sizes though, would take more investigation.

# Check out p-values for actual distributions
# should be approximately uniform
# On my machine, takes about 3 minutes to 
# crunch through 100 simulations
# So this took me ~5 hours
res_p = []
for i in range(10000):
    if (i % 100) == 0:
        print(f'Sim {i} @ {datetime.now()}')
    mu = np.random.uniform(low=5,high=1000,size=1)[0]
    si = np.random.randint(low=10,high=100,size=1)[0]
    simloc = poisson.rvs(mu,size=si)
    ks,pv,sv = lill_poisson(simloc)
    res_p.append(pv)

Caveat emptor, I do not know the power of this relative to the binning Chi-square approach. But here is how I would do the Chi-square approach (I don't believe the approach you did is correct). Here I bin according to Poisson quantiles, instead of based on the data. (So the expected number per bin is the same.)

# Chi-square approach bins
# Use quintiles of the hypothetical Poisson
df = pd.DataFrame(obs,columns=['counts'])
df['quantile'] = poisson.cdf(obs.mean(),obs)
df['quin'] = np.floor(df['quantile']/0.2)
obs_counts = df['quin'].value_counts()
exp_counts = len(obs)/5
chi_stat = ((obs_counts - exp_counts)**2/exp_counts).sum()
Chi-square value of 6.66

Like I said, different binning strategies will give different p-values. Here if you do chisquare(obs_counts) or reduce the degrees of freedom by one, chisquare(obs_counts,ddof=1), it still results in a p-value > 0.05. If you do 10 bins in this approach with this data, the p-value gets larger.

All in all, I think your example data is quite consistent with a Poisson distribution.