Compute BIC clustering criterion (to validate clusters after K-means)

Question

I'm wondering if there is a good way to calculate the clustering criterion based on BIC formula, for a k-means output in R? I'm a bit confused as to how to calculate that BIC so that I can compare it with other clustering models. Currently I'm using the stats package implementation of k-means.

Answer 1

To calculate the BIC for the kmeans results, I have tested the following methods:

1. The following formula is from: [ref2]

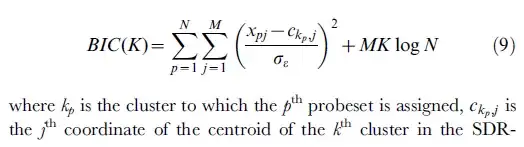
The r code for above formula is:

  k3 <- kmeans(mt,3)
  intra.mean <- mean(k3$within)
  k10 <- kmeans(mt,10)
  centers <- k10$centers
  BIC <- function(mt,cls,intra.mean,centers){
    x.centers <- apply(centers,2,function(y){
      as.numeric(y)[cls]
    })
    sum1 <- sum(((mt-x.centers)/intra.mean)**2)
    sum1 + NCOL(mt)*length(unique(cls))*log(NROW(mt))
  }
#

the problem is when i using the above r code, the calculated BIC was monotone increasing. what's the reason?

[ref2] Ramsey, S. A., et al. (2008). "Uncovering a macrophage transcriptional program by integrating evidence from motif scanning and expression dynamics." PLoS Comput Biol 4(3): e1000021.

2. I have used the new formula from https://stackoverflow.com/questions/15839774/how-to-calculate-bic-for-k-means-clustering-in-r

   BIC2 <- function(fit){
   m = ncol(fit$centers)
       n = length(fit$cluster)
   k = nrow(fit$centers)
       D = fit$tot.withinss
   return(data.frame(AIC = D + 2*m*k,
                     BIC = D + log(n)*m*k))
   }
   

This method given the lowest BIC value at cluster number 155.

3. using @ttnphns provided method, the corresponding R code as listed below. However, the problem is what the difference between Vc and V? And how to calculate the element-wise multiplication for two vectors with different length?

   BIC3 <- function(fit,mt){
   Nc <- as.matrix(as.numeric(table(fit$cluster)),nc=1)
   Vc <- apply(mt,2,function(x){
       tapply(x,fit$cluster,var)
    })
   V <- matrix(rep(apply(mt,2,function(x){
   var(x)
   }),length(Nc)),byrow=TRUE,nrow=length(Nc))
   LL = -Nc * colSums( log(Vc + V)/2 ) ##how to calculate this? elementa-wise multiplication for two vectors with different length?
   BIC = -2 * rowSums(LL) + 2*K*P * log(NRoW(mt))
   return(BIC)
   }
   

Answer 2

I don't use R but here is a schedule which I hope will help you to compute the value of BIC or AIC clustering criteria for any given clustering solution.

This approach follows SPSS Algorithms Two-step cluster analysis (see the formulas there, starting from chapter "Number of clusters", then move to "Log-likelihood distance" where ksi, the log-likelihood, is defined). BIC (or AIC) is being computed based on the log-likelihood distance. I'm showing below computation for quantitative data only (the formula given in the SPSS document is more general and incorporates also categorical data; I'm discussing only its quantitative data "part"):

X is data matrix, N objects x P quantitative variables.
Y is column of length N designating cluster membership; clusters 1, 2,..., K.
1. Compute 1 x K row Nc showing number of objects in each cluster.
2. Compute P x K matrix Vc containing variances by clusters.
   Use denominator "n", not "n-1", to compute those, because there may be clusters with just one object.
3. Compute P x 1 column containing variances for the whole sample. Use "n-1" denominator.
   Then propagate the column to get P x K matrix V.
4. Compute log-likelihood LL, 1 x K row. LL = -Nc &* csum( ln(Vc + V)/2 ),
   where "&*" means usual, elementwise multiplication;
   "csum" means sum of elements within columns.
5. Compute BIC value. BIC = -2 * rsum(LL) + 2*K*P * ln(N),
   where "rsum" means sum of elements within row.
6. Also could compute AIC value. AIC = -2 * rsum(LL) + 4*K*P
Note: By default SPSS TwoStep cluster procedure standardizes all
quantitative variables, therefore V consists of just 1s, it is constant 1.
V serves simply as an insurance against ln(0) case.

AIC and BIC clustering criteria are used not only with K-means clustering. They may be useful for any clustering method which treats within-cluster density as within-cluster variance. Because AIC and BIC are to penalize for "excessive parameters", they unambiguously tend to prefer solutions with less clusters. "Less clusters more dissociated from one another" could be their motto.

There can be various versions of BIC/AIC clustering criteria. The one I showed here uses Vc, within-cluster variances, as the principal term of the log-likelihood. Some other version, perhaps better suited for k-means clustering, might base the log-likelihood on the within-cluster sums-of-squares.

The pdf version of the same SPSS document which I referred to.

And here is finally the formulae themselves, corresponding to the above pseudocode and the document; it is taken from the description of the function (macro) I've written for SPSS users. If you have any suggestions to improve the formulae please post a comment or an answer.