Let:
Standard deviation of random variable $A =\sigma_{1}=5$
Standard deviation of random variable $B=\sigma_{2}=4$
Then the variance of A+B is:
$Var(w_{1}A+w_{2}B)= w_{1}^{2}\sigma_{1}^{2}+w_{2}^{2}\sigma_{2}^{2} +2w_{1}w_{2}p_{1,2}\sigma_{1}\sigma_{2}$
Where:
$p_{1,2}$ is the correlation between the two random variables.
$w_{1}$ is the weight of random variable A
$w_{2}$ is the weight of random variable B
$w_{1}+w_{2}=1$
The figure below plots the variance of A and B as the weight of A changes from 0 to 1, for the correlations -1 (yellow),0 (blue) and 1 (red).
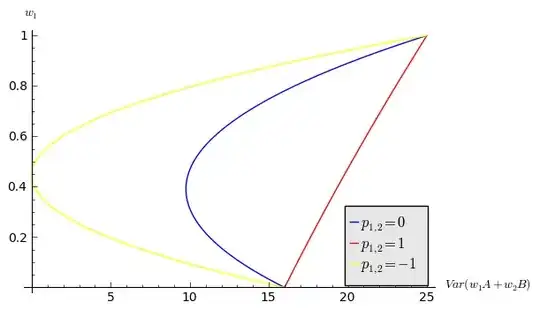
How did the formula result in a straight line (red) when the correlation is 1? As far as I can tell, when $p_{1,2}=1$, the formula simplifies to:
$Var(w_{1}A+w_{2}B)= w_{1}^{2}\sigma_{1}^{2}+w_{2}^{2}\sigma_{2}^{2} +2w_{1}w_{2}\sigma_{1}\sigma_{2}$
How can I express that in the form of $y=mx+c$?
Thank you.
