Say we have a graph between number of people vs income. Say there is a majority of people with income 20000$ and as we go on increasing the income the number of people gets lower and lower. That means this data is positively skewed.
But what is the reason that this is positively skewed? Why are real life data skewed at all?
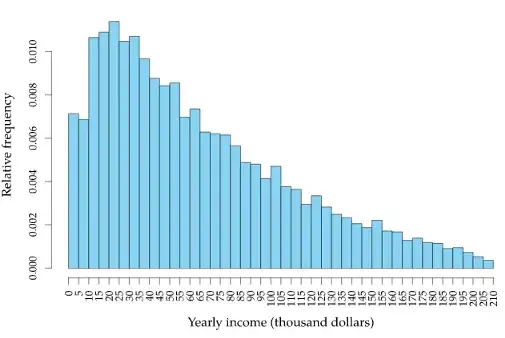
-
Income data is very skewed is because of Pareto Principle or law of vital few see Wiki. – forecaster Jul 31 '21 at 04:34
2 Answers
Symmetry is a pretty strict condition and would be very rarely the case in real data (if ever).
Even near-symmetry is not that common. Most distributions are not really close to symmetric.
The support of distributions (loosely, what values the random variable can take) is often suggestive of the likely direction of potential skewness.
There's no real upper limit on income but a pretty definite lower limit. Income in particular can't be negative - aside some special edge cases perhaps.
It's pretty easy to find people who earn more than twice the mean (income$>μ+μ$) but not people who earn equally as far below the mean (income$<μ−μ$), so we can immediately see that if that's the case, it cannot be symmetric. Similarly you could find people who earn 3 or 4 times the mean, but not the other direction.
Many measured quantities are similar (consider weight, say), you can weigh more than twice the average but not equally as far below the mean.
Similarly with counts of events; you can't have fewer than 0 events but in many cases you can have more than twice the mean; in those cases you would expect asymmetry.
Note that many effects on expected income are more-or-less multiplicative, rather than additive (their logs are additive). The combined result of several multiplicative effects tends to produce right skew distributions.
You do see left skewness -- consider for example, scores on an easy test, where many people score close to full marks, but some people don't do all that well. Conversely, scores on a hard test might be right skew. There, considering where typical values are relative to the support gives a clue about the likely direction of skewness.
- 282,281
-
2Yeah, we do occasionally get negative incomes for accounting reasons (e.g. somebody buys shares and then sells them back for less than the purchase price) but it's uncommon, and not nearly enough to balance out high-earners. – GB supports the mod strike Jul 31 '21 at 05:01
In most cases, there's no particular reason to expect a symmetric distribution.
The Central Limit Theorem tells us that certain kinds of phenomena will generate approximately symmetric distributions - roughly speaking, when we add a large number of independent components that are each small relative to the whole. If I took a million people, and got them each to put a thousand dollars a day through one-dollar slot machines (each with a 97% payoff), their annual incomes would show a very nearly symmetric distribution.
But in real life, many of the things we measure aren't produced by processes that satisfy the CLT's assumptions, so there's no particular reason to expect that they should be symmetrical.
In the case of income, there are several things going on that tend to produce skewed distributions:
- Money makes money: the more you have, the more opportunities you have to make and save money. You can buy the fifty-dollar boots that last ten years instead of the ten-dollar boots that fall apart after a year. You can feed yourself and still have money left over to invest in the stock market, or on a nice suit to boost your chances of getting a higher-paying job. And so on. Because of this, it's easier to turn USD1000,000 into USD1001,000 than it is to turn 1000 into 2000, so the right-hand tail of that distribution stretches out longer.
- When this kind of phenomenon is driving skewness, applying a log transformation will often give you a much more symmetrical distribution.
- There are "lumps" in the distribution. The obvious one is the large group of people who don't have an income at all, e.g. children or stay-at-home partners, but if you looked closely at the data you'd discover others corresponding to things like minimum wage rates, standard government pensions, and so forth. When these "lumps" are created, there is no mechanism to create a matching lump on the other side of the mean/median income to restore symmetry.
- As noted already by Glen_b, many distributions are bounded below by zero, and have either no upper bound, or an upper bound which is more than twice the mean/median value. In these cases it is impossible for the distribution to be symmetric.
- Often the mathematical relationship between two quantities of interest means that they can't all have symmetrical distributions. For example, suppose you are measuring the radius of ball-bearings produced at a factory, and I'm measuring the volume (which scales as the cube of radius). If the distribution of the radius is symmetric (which requires that mean = median), and if there is any variance at all in this distribution, then the mean volume will be larger than the median volume, so volume must be asymmetric.