4

In hypothesis testing using a frequentist approach, we usually compute a p-value = $P(data\ or\ more\ extreme | H0)$.

Moving to a bayesian approach, we are then able to compute different things, such as $P(H0 | data)$.

Suppose I have two biased coins $A$ and $B$ with heads probabilities $p(A)$, $p(B)$:

$H0: p(A) <= p(B)$

$H1: p(B) > p(A)$

I flip $N$ times each coin, observing number of heads $H(A)$ and $H(B)$. With this info I can go on the compute a p-value giving $P(data | H0) = P(H(A), H(B) | p(A)<=p(B))$.

Moving with a bayesian approach, assuming $\theta_A$ and $\theta_B \sim Beta$, we can get the Posteriors $\theta_A \sim Beta(H(A),N-H(A))$ and $\theta_B \sim Beta(H(B),N-H(B))$. We can then compute $P(H0 | data) = P(p(A)<=p(B) | H(A), H(B))$.

I would expect these to not be the same, but doing a quick simulation in python:

from scipy.stats import beta, norm
import numpy as np

N = 100
sample_size = 100000


for H_A, H_B in zip(np.random.randint(1,N,N), np.random.randint(1,N,N)):
    a_beta = beta(H_A, N-H_A)
    b_beta = beta(H_B, N-H_B)
    prob = (a_beta.rvs(sample_size) > b_beta.rvs(sample_size)).mean()
    z = (H_A/N - H_B/N)/np.sqrt((H_A/N(1-H_A/N)/N) + (H_B/N(1-H_B/N)/N))
    print(round(prob, 3), "\t", round(norm.cdf(z),3))


"""
1.0      1.0
1.0      1.0
0.0      0.0
0.132    0.133
0.001    0.001
0.0      0.0
0.0      0.0
1.0      1.0
1.0      1.0
0.0      0.0
0.742    0.74
1.0      1.0
0.0      0.0
1.0      1.0
0.127    0.129
1.0      1.0
0.953    0.952
...
"""
jcp
  • 521
  • 2
    Note that in frequentist analysis the parameters and hypotheses are not random variables, so it's technically wrong to write $P(data|H0)$, because this suggests that it's a conditional probability based on the random variable H0 taking a certain value. It's more correct to write $P_{H0}(data)$, as this says that it's the unconditional probability of the data assuming that H0 is true. Consequently no frequentist analysis will give you a probability that H0 is true (the p-value is definitively not such a probability), because such a probability is not defined in frequentism. – Christian Hennig Jul 21 '21 at 09:58
  • 3
    The p-value may happen to be equal or approximately equal to a Bayesian probability that H0 is true given a certain prior, but still according to frequentist logic it is something essentially different. – Christian Hennig Jul 21 '21 at 10:00

1 Answers1

1

First of all, I guess we can agree that if different statistical methods give the same results for the same data, it's a kind of good, isn't it? It means that there's nothing fancy about the data or the methods.

Second, you are not using any prior. Technically, you could consider this code to be implicitly using an "uninformative" Haldane prior, i.e. one with $\alpha=\beta=0$ in a beta-binomial model. Such prior would soon get overwhelmed with the data and give results nearly the same as when maximizing the likelihood function alone.

The posteriors would have the expected values $E[A] = H(A)/N$ and $E[B] = H(B)/N$ respectively. In your two-sample $z$-test you are comparing the difference between $H(A)/N$ and $H(B)/N$ as well, so looking at the same thing. Recall that $E[A] - E[B] = E[A - B]$, so otherwise that you are using a normal approximation in the second case, you expect them to be the same.

The results are so close because of three things that hold: (a) the prior is very "weak", so it has a small influence on the result, (b) the sample size N is relatively big, so it overwhelmed the prior, and (c) because of sample size is relatively big, the normal approximation works quite well. If you tried something like N=5 the differences would be more clear. Notice however that while both approaches gave similar results, they are based on completely different assumptions and have different interpretations, so in general, should not be thought of as exchangeable.

Code example

Below you can see your code modified so that it also produces the plots of the beta distributions vs the normal approximations.

from scipy.stats import beta, norm
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)


N = 5
R = 10
sample_size = 100_000


def beta_std(α, β):
    v = (α * β) / ((α + β)*2  (α + β + 1))
    return np.sqrt(v)


for H_A, H_B in zip(np.random.randint(1,N,R), np.random.randint(1,N,R)):


a_beta = beta(H_A, N-H_A)
b_beta = beta(H_B, N-H_B)
prob = (a_beta.rvs(sample_size) &gt; b_beta.rvs(sample_size)).mean()
z = (H_A/N - H_B/N)/np.sqrt((H_A/N*(1-H_A/N)/N) + (H_B/N*(1-H_B/N)/N))
print(round(prob, 3), &quot;\t&quot;, round(norm.cdf(z),3))

x = np.linspace(0, 1, 500)
fig, (ax1, ax2) = plt.subplots(1, 2)

mean_A = H_A/N
std_A = beta_std(H_A, N-H_A)

ax1.plot(x, a_beta.pdf(x), label=&quot;beta&quot;)
ax1.plot(x, norm(loc=mean_A, scale=std_A).pdf(x), label=&quot;normal approx&quot;)
ax1.set_title(f&quot;H(A)={H_A}&quot;)
ax1.legend()

mean_B = H_B/N
std_B = beta_std(H_B, N-H_B)

ax2.plot(x, b_beta.pdf(x), label=&quot;beta&quot;)
ax2.plot(x, norm(loc=mean_B, scale=std_B).pdf(x), label=&quot;normal approx&quot;)
ax2.set_title(f&quot;H(B)={H_B}&quot;)
ax2.legend()

With a small sample size N=5, the approximation is not perfect:

Normal approximation vs beta distribution, as produced with the code above with N=5.

However, if you increase it to N=100, it is very close:

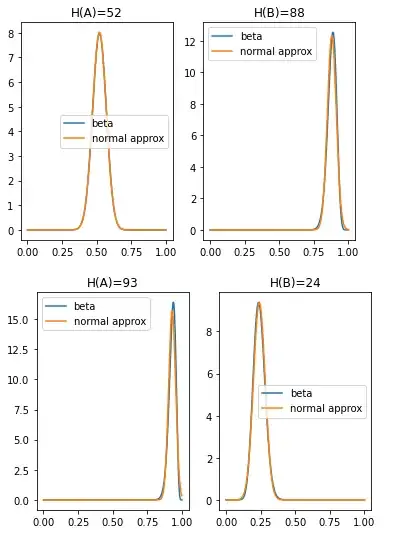
As above, but using N=100.

No wonder you get nearly the same results. More than this, the distribution of the difference between the random variables is even better approximated by a normal distribution, not to unnecessarily extend the answer, I made a notebook illustrating this.

Tim
  • 138,066
  • I understand that I'm comparing expected values but, as far as I understood, in the z-test I'm getting the prob that H0 is true given the differences of means (and std), while in the bayesian approach I estimate the distribution of the data and then compute the probability that H0 is true. My confusion comes from seeming to get P(H0|data) = P(data|H0) – jcp Jul 21 '21 at 07:43
  • 1
    @jcp Edited second paragraph for this. You are not using a flat prior, but other "uninformative" prior, but let's say you used a flat prior $p(\theta) \propto 1$ then $p(\theta|X) \propto p(X|\theta) \times 1 = p(X|\theta)$. With other "uninformative" priors it's not exactly the same, but very close. Simply: with an "uninformative" prior posterior is nearly the same as likelihood. – Tim Jul 21 '21 at 07:46
  • But does that mean then that a p-value is almost equivalent to the posterior an uninformative prior? I can then interpret a p-value is virtually the probability that the H0 is true? – jcp Jul 21 '21 at 08:10
  • 2
    @jcp no, see https://stats.stackexchange.com/questions/341553/what-is-bayesian-posterior-probability-and-how-is-it-different-to-just-using-a-p or https://stats.stackexchange.com/questions/275527/using-p-value-to-compute-the-probability-of-hypothesis-being-true-what-else-is/275547#275547 Frequentist and Bayesian methods can give same or vary similar results in some cases but are not the same and their interpretation is different. – Tim Jul 21 '21 at 08:42
  • That's what I would expect. But: in my example, all possibilities of the test using a beta-binomial model with a "Haldane prior" leads $P(H0 | data) \tilde= P(data | H0)$. That leads me to believe that any classic p-value from a hypothesis test with Bernoulli random variables can be interpreted as approximately $P(H0 | data)$ with an Haldane prior – jcp Jul 21 '21 at 09:16
  • @jcp that's an overstatement. Keep in mind that no prior is truly "uninformative" and that in the $z$-test uses the normal approximation, not the exact distribution. For a counterexample, just change N=5 or a smaller value. Additionally, plot the beta distribution pdf's vs the normal approximation's and you'll see that they do differ. It's just a simple case and relatively large data for relatively weak prior, so both prior has small impace and the normal approximation works well enough. – Tim Jul 21 '21 at 09:22
  • Fair enough, but still it blows my mind that this is true under large amounts of data. Working out the math, I get to the point where if the priors are the same, $P(H0)$ and $P(H1)$ cancel out and I'm left with $P(H0|data) = p(data | H0)/(p(data | H0) + p(data | H1))$, which 1-only works out if $p(data | H0) + p(data | H1) = 1$ and 2-is independent on the prior choices – jcp Jul 21 '21 at 09:48
  • @jcp I added an example on the bottom of the answer for clarity. As for "the math" it sounds like something for a separate question. If your math tells you that the distribution of independent random variables is the same as if they were dependent, then by definition something is wrong. – Tim Jul 21 '21 at 09:55
  • I don't see the utility in this exercise. As others have eloquently said frequentism does not even conceive of probabilities that are not limits of long-term frequencies of event occurrences. And the equivalence only holds in a very special case where the sample size is fixed and there is exactly one look at the data. – Frank Harrell Jul 21 '21 at 11:15
  • @FrankHarrell it merely answers "why" the observed results ended up close. It was already explained in the comments that they in essence are different, though I edited the answer to make it explicit. – Tim Jul 21 '21 at 12:00
  • 1
    I'm implying that it is not relevant to know this in such a highly specialized case. But you said it well. We need to also keep the "fixed sample size one look" in every comparison. But the bottom line is that if you believe that probabilities do not need to be relative frequencies, be Bayesian and don't try to jump back and forth. If you believe that the only basis for probabilities is frequencies, then don't attempt any comparison because Bayes has to be meaningless to you. – Frank Harrell Jul 21 '21 at 15:32