2

I'm trying to find a function that matches the following shape.

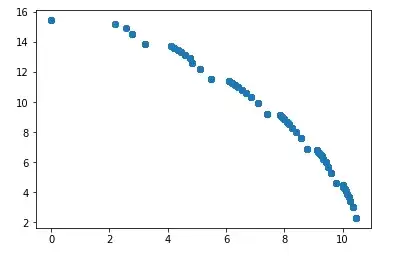
enter image description here

My first attempt was with a cosine function

$$ f(x) = a\cos(b x)$$

which yields the following result:

enter image description here

What modification of the cosine function could help to make it better fit the required shape? Any ideas or suggestions are appreciated.

EDIT: the raw data is available in csv format here.

Galen
  • 8,442
jak
  • 121
  • 4
  • 4
    If you connect the dots, you'd get a perfect fit. What exactly are you trying to do? What is this data? Could you attach the raw data in text format to the question? – Tim Jul 15 '21 at 09:25
  • @Tim I'm trying to understand the relationship between the rank and the number of installs in different app stores. The data here shows the Log(rank) over the Log(number of installs) for Wordpress plugins. I want to find a function that matches the general shape and then see if it applies to other app stores as well. – jak Jul 15 '21 at 09:31
  • I also added a link to the data to the question. – jak Jul 15 '21 at 09:36
  • I cannot load your data. Could you attach the data in a more standard format. – JJacquelin Aug 12 '21 at 06:59

1 Answers1

1

(sorry i cant comment yet

0. Getting original plot

i tried to download data in r, but couldnt get to get your plot

i named data rss

tried, not good

plot(log(rss$rank)/log(rss$installs))
plot(log(rss$installs)/log(rss$rank))

working

plot(log(rss$rank), log(rss$installs))

thanks / credit at comment section

1. Data and model trying

I tried, just get data

 xx=(log(rss$rank) )
 yy=log(rss$installs)

zz=cbind(xx,yy) #matrix
zz2 <- zz[!is.infinite(rowSums(zz)),] #remove inf values

then trying fit linear reg. with poly function (simple curve

lii= (  lm(zz2[,2]~poly(zz2[,1] ,223, raw = TRUE) ) )

plot(zz2[,1],zz2[,2])
lines(zz2[,1],lii$fitted.values ,col="green")

Started with 1, as "better fit" .. appeared at 223

List of poly parameter value

[1] 1
[1] 2
[1] 3
[1] 4
[1] 5
[1] 6
[1] 7
[1] 8
[1] 9
[1] 10
[1] 158
[1] 159
[1] 161
[1] 172
[1] 174
[1] 176
[1] 178
[1] 209
[1] 223

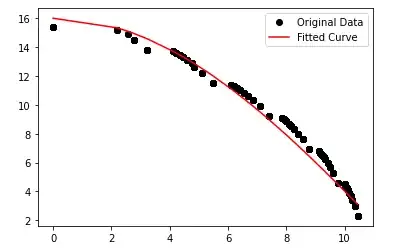
Final graph enter image description here Last point before x=4 has bad fit, so maybe some hardcoding needed as replacement.

Anyway, this is very very bad solution done by overfitting polynoms :D, but someone maybe found it iterested.

user2120
  • 63