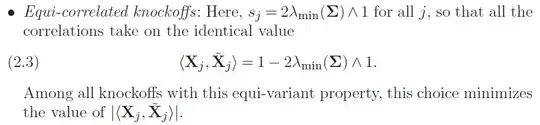I'm trying to understand certain results stated in the original Knockoff paper ("Fixed-X").
They state that the Knockoffs can be constructed as follows:
It's true that this matrix obeys the properties needed from Knockoffs, though I wonder how they got to it in the first place?
More importantly, they want to maximize the $s_j$ - and offer 2 solutions. Regarding the equi-correlated solution ($s_j$'s are equal to each other), why is it that $s_j=\min(1,2\lambda_{min}(\Sigma))$?
Ok, figured it out with a help of a professor of mine:
We want to maximize the vector $s$ given that all it's elements are equal. So the problem is actually:
$$\max \{ s: 2 \Sigma \succeq diag (se), s \geq 0\}$$
Where $e$ is a vector of 1's, and $s\in\mathbb R$ (a scalar). The Loewer order constraint comes from the fact that we want G to be PSD - and using Schur complement. You can check here for more detail.
This is equivalent to:
$$\max \{ s: 2 \Sigma \succeq s I, s \geq 0\}$$
Now, basic Linear Algebra tells us that $$2 \Sigma \succeq s I \iff 2\lambda_{\min}(\Sigma) \geq s$$
This is because $2 \Sigma \succeq s I \iff 2 \Sigma - s I\succeq 0 \iff \lambda_{min}(2 \Sigma - s I)\ge 0$.
The eigenvalue operator of adding/subtracting an identity matrix is "linear" in a sense, i.e. $\lambda_{min}(2 \Sigma - s I)=\lambda_{min}(2 \Sigma) - s = 2\lambda_{min}(\Sigma) -s$.
So $\lambda_{min}(2 \Sigma - s I)\ge 0 \iff 2\lambda_{min}(\Sigma) \ge s$.
So the problem reduces to: $$\max \{ s: 0 \leq s \leq 2 \lambda_{\min}(\Sigma)\}$$ And the obvious solution is then: $$s=2 \lambda_{\min}(\Sigma)$$
Since we also don't want to go below 0 in the correlation between a knockoff and an original feature, as that would counter the point, we take the minimum of the $s_j$ and 1.