1

Monthly grid-cell burned area estimates are (almost) lognormally distributed, censored at a fuzzy threshold and zero-inflated. I want to predict burned area from weather etc. About 40% of the observations are zero. Some zeroes are due to true lack of fire. Others are due to the limits of satellite detection. Detection capability and therefore minimum detected burned area varies with both fire intensity and size, complicated by cloud cover, overpass frequency etc.

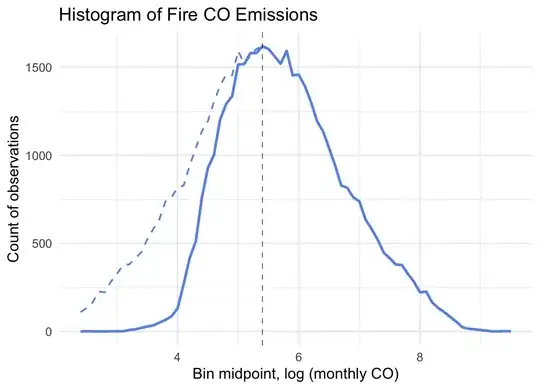
Judged visually, the following histogram of log-transformed continuous non-zero burned area (actually fire CO emissions, but it could be burned area) looks nicely normal for the upper, say, 60% of data values. The dotted line is mirrored values around the mode, as a presumed target to describe the true distribution, or one to explore. For smaller values one can imagine a sort of missing ‘bite’, maybe 20% of the observations. The presumed missing observations add up to little burned area but omitting them would bias the regression. Again just visually, it appears that a normally distributed addition stacked onto the histogram would provide rough bilateral symmetry. So maybe just two additional parameters could capture the threshold‘s variability.

Histogram of Non-Zero Observations

The zero inflation with two possible causes seems suited to tools like r’s mhurdle or crch. But those commands require a crisp censoring threshold. I’d prefer to use existing commands. If that isn’t possible then one might (with difficulty!) build a custom Bayesian solution. I think a somewhat variable detection limit is common in satellite data. So I imagine, with hope, that others have worked on approaches for data like this.

kjetil b halvorsen
  • 77,844
InColorado
  • 143
  • 1
  • 6

1 Answers1

2

Ordinal semiparametric regression models such as the proportional odds model can handle arbitrarily large zero inflation, all the way to the extreme case where Y takes on only two values (this reduces to binary logistic regression). Ordinal regression automatically handles detection limits if the limits are at or beyond the really observed data. When detection limits are interior to the data you need to formally incorporate left, right, or interval censoring into the likelihood calculations. The blrm function in the R rmsb package can fit a Bayesian proportional odds model with arbitrary censoring, as exemplified by one of the examples linked from that site.

Frank Harrell
  • 91,879
  • 6
  • 178
  • 397
  • The “semiparametric” used here together with the binary logistic function being able to handle zero inflation, suggests for the binary case you are referring to a model different from that provided by the R glm function? Rephrased, I am unsure why semiparametric was used in the first sentence. – Single Malt Apr 02 '21 at 13:51
  • Semiparametric ordinal models are unified in that you don't need a separate binary logistic model for the zeros. In R you can use these package::functions : rms::lrm, rms::orm, rmsb::blrm, stats::polr. The orm function is very efficient when you have lots of distinct Y values. Semiparametric = having an intercept parameter for each distinct Y, less 1. So fits any distribution, even bimodal ones with discontinuities. – Frank Harrell Apr 02 '21 at 18:09
  • This is a helpful, I am beginning to understand this. I had overlooked rms::lrm and rms::orm, with the former I had assumed was just an alternative to glm but perhaps using rms syntax. Whereas it seems they let the data influence the model more by calculation of the intercept parameters, thus having advantages such as eliminating zero inflation workarounds if needed. Is this a correct summary? Does rms::lrm give you distinct Y minus 1 extra parameters in the model compared with standard R glm? – Single Malt Apr 02 '21 at 20:02
  • 1
    Yes to both. You can't do the proportional odds and related semiparametric models with glm. That's why polr has been around a long time in R. I was wrong about the location. polr is in MASS. – Frank Harrell Apr 02 '21 at 21:12