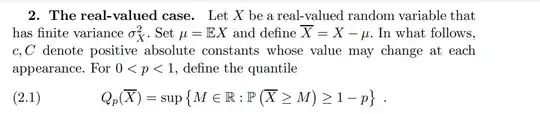I'm specifically having trouble understanding this paragraph and most of the notation. If someone could explain what $EX$, $X$ bar, and the whole quantile definition meant that would be great.
Asked
Active
Viewed 74 times
1
-
1$\mathbb E X$ is the expectation of $X$. Here $\overline X$ seems to be explicitly defined so that it is $X$ relocated with its expectation being zero; that is not the common use and without an explicit definition might often be used to signify the sample average. The quantile definition is essentially what you might hope: $Q_{0.25}(\overline{X})$ is the lower quartile, i.e. the largest value which at least three-quarters of the distribution of $\overline{X}$ exceeds or equals – Henry Jan 27 '21 at 00:15
-
2To summary the comment by @Henry: these are standard definitions and standard notation, which means you can learn about them by consulting textbooks, especially those that aim at mathematical rigor and are fairly modern (published since 1950 or so). – whuber Jan 27 '21 at 15:00
-
@Henry, if you wish you can make that as answer. Otherwise I would make a CW answer with your and whuber's comments. – User1865345 Dec 12 '23 at 15:08
-
Some questions which will help to understand this one: https://stats.stackexchange.com/questions/177728/how-i-can-get-a-quantile-function-of-a-discrete-distribution-like-the-binomial, https://stats.stackexchange.com/questions/593980/compute-the-quantile-function-of-this-distribution, https://stats.stackexchange.com/questions/465359/quantile-function-confusion-about-min-x-text-fx-geq-p, https://stats.stackexchange.com/questions/562936/there-are-many-different-quantile-definitions-what-diffrentiates-and-motivates – kjetil b halvorsen Dec 12 '23 at 15:24
-
1@User1865345 This question was closed just before you asked - so it is not currently possible. If that changes (I do not think it should) then anyone can feel free to give an answer – Henry Dec 12 '23 at 15:36
-
Ah. I see, whuber closed it (correctly) @Henry. – User1865345 Dec 12 '23 at 15:59