Computing the decision boundary of a linear SVM model

Question

Given the support vectors of a linear SVM, how can I compute the equation of the decision boundary?

Answer 1

The Elements of Statistical Learning, from Hastie et al., has a complete chapter on support vector classifiers and SVMs (in your case, start page 418 on the 2nd edition). Another good tutorial is Support Vector Machines in R, by David Meyer.

Unless I misunderstood your question, the decision boundary (or hyperplane) is defined by $x^T\beta + \beta_0=0$ (with $\|\beta\|=1$, and $\beta_0$ the intercept term), or as @ebony said a linear combination of the support vectors. The margin is then $2/\|\beta\|$, following Hastie et al. notations.

From the on-line help of ksvm() in the kernlab R package, but see also kernlab – An S4 Package for Kernel Methods in R, here is a toy example:

set.seed(101)
x <- rbind(matrix(rnorm(120),,2),matrix(rnorm(120,mean=3),,2))
y <- matrix(c(rep(1,60),rep(-1,60)))
svp <- ksvm(x,y,type="C-svc")
plot(svp,data=x)

Note that for the sake of clarity, we don't consider train and test samples. Results are shown below, where color shading helps visualizing the fitted decision values; values around 0 are on the decision boundary.

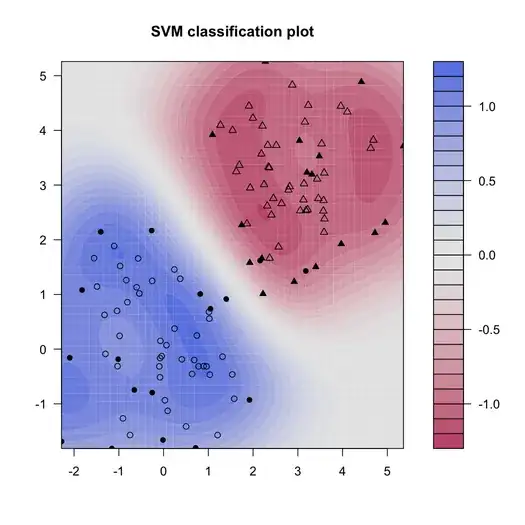
Calling attributes(svp) gives you attributes that you can access, e.g.

alpha(svp)  # support vectors whose indices may be 
            # found with alphaindex(svp)
b(svp)      # (negative) intercept 

So, to display the decision boundary, with its corresponding margin, let's try the following (in the rescaled space), which is largely inspired from a tutorial on SVM made some time ago by Jean-Philippe Vert:

plot(scale(x), col=y+2, pch=y+2, xlab="", ylab="")
w <- colSums(coef(svp)[[1]] * x[unlist(alphaindex(svp)),])
b <- b(svp)
abline(b/w[1],-w[2]/w[1])
abline((b+1)/w[1],-w[2]/w[1],lty=2)
abline((b-1)/w[1],-w[2]/w[1],lty=2)

And here it is:

Answer 2

It's a linear combination of the support vectors where the coefficients are given by the Lagrange multipliers corresponding to these support vectors.