0

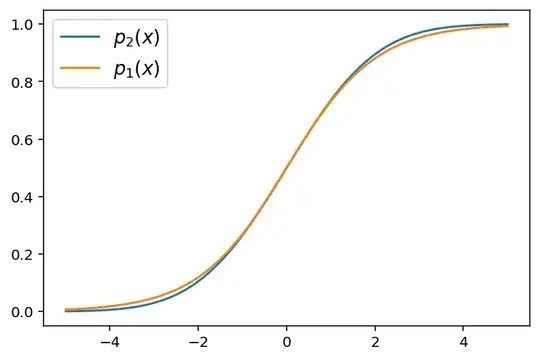
Imagine an experiment, in which an observer has to discriminate between two stimulus categories at different contrast levels $|x|$. As $|x|$ becomes lower, the observer will be more prone to making perceptual mistakes. The stimulus category is coded in the sign of $x$. I'm interested in the relationship between two different ways of modeling the observer's "perceptual noise" based on their choices in a series of stimulus presentations.

The first way would be to fit a logistic function

$ p_1(x) = \frac{1}{1+e^{-\beta\cdot x}} $

where $p_1(x)$ is the probability to choose the stimulus category with positive signs ($S^+$). Here, $\beta$ would reflect the degree of perceptual noise.

A second way would be to assume that the observer has Gaussian Noise $\mathcal{N}(0,\sigma)$ around each observation of $x$ and then compute the probability to choose $S^+$ by means of the cumulative probability density function as follows:

$ p_2(x) = \frac{1}{\sigma\sqrt{2\pi}}\int\limits_{-\infty}^{x}e^{-\frac{z^2}{2\sigma^2}} dz $

In this case, $\sigma$ would be an estimate of the perceptual noise.

I have a hunch that both these approaches are intimately related, but I'm not sure how. Is it an underlying assumption of the logistic function that the noise is normally distributed? Is there a formula that describes the relationship between $\beta$ of $p_1(x)$ and $\sigma$ of $p_2(x)$? Are, in the end, $p_1(x)$ and $p_2(x)$ essentially identical and could $p_1$ be derived from $p_2$?

Gerardo Duran-Martin
  • 580
monade
  • 509
  • Probabilities are bounded to $[0, 1]$ while normal distribution is unbounded $(-\infty, \infty)$, so probability + Gaussian noise is not probability any more since it goes outside the bounds... What exactly do you mean by their relation? – Tim Aug 18 '20 at 13:47
  • Where did you see probability + Gaussian noise? My assumption is that there is Gaussian noise around each observation $x$, where $x$ is the stimulus variable, not a probability. – monade Aug 18 '20 at 13:49
  • Than what you mean by "relation" between them? You could pick arbitrary $\sigma$ to generate $x$ and then multiply it by another arbitrary $\beta$ and use logistic transformation to generate such data, so both can be completely independent from each other. – Tim Aug 18 '20 at 13:56
  • I had a typo in $p_2(x)$, maybe things become more clear now. – monade Aug 18 '20 at 13:57
  • I'm not sure what you mean by $p_2$ in here. What exactly this ought to be? – Tim Aug 18 '20 at 13:59
  • $p_2$ is the probability of choosing the positive stimulus category, given an observation $x$. The idea is that I fit both models ($p_1$ and $p_2$) to the choice data and obtain values for β and σ. One question would be whether the expected values of β and σ are related in terms of a formula. – monade Aug 18 '20 at 14:01
  • 1
    I now realize your misunderstanding. $p_1$ and $p_2$ are two alternatives to achieve the same thing: modeling noisy perceptual choices. (your first question sounded like you thought that I add Gaussian noise p2 on top of the choice probabilities of p1, which of course would not make sense) – monade Aug 18 '20 at 14:13
  • 3
    If I follow you correctly, you are asking how logit and probit models might be related. Although the mathematical relationship is not simple, in practice they behave so similarly that they are considered interchangeable. Replacing the Gaussian error by a double exponential ("Laplacian") error makes the two approaches equivalent. Perhaps your questions are all satisfactorily addressed at https://stats.stackexchange.com/questions/20523/difference-between-logit-and-probit-models? – whuber Aug 20 '20 at 16:31
  • Thanks, this question is an excellent resource. The double exponential error would be $\frac{e^{-x}}{(1 + e^{-x})^2}$ (using the notation of my question)? – monade Aug 20 '20 at 16:47
  • 1
    The double exponential distribution is the location-scale family determined by the distribution with density function $f(x)=\exp(-|x|)/2.$ – whuber Aug 20 '20 at 17:51
  • See also https://stats.stackexchange.com/questions/403575/how-is-logistic-regression-related-to-logistic-distribution/403885#403885 – kjetil b halvorsen Aug 27 '20 at 14:14

1 Answers1

2

The first way to model the value $p_1(x)$ is via the sigmoid function; the second way to model it, namely $p_2(x)$, is via the probit function.

They are not intimately related per se, i.e., one cannot naturally get from the sigmoid to the probit or vice-versa. However, the probit function can be used as an approximation to the sigmoid function. In fact, the two functions are closest, around $x=0$, when $p_1(x)$ is approximated by $p_2$ as $p_2\left(\sqrt{\frac{\pi}{8}}x\right)$.

probit-vs-logistic

This is useful, for instance, in the context of bayesian logistic regresion, where we are required to solve an integral of the form

$$ \int_{\mathbb{R}} p_1(x) \mathcal{N}(x\vert\mu_x, \sigma_x) dx $$

Using the sigmoid function $p_1(x)$ makes the integral intractable, but we can make a variational approximation to the integral considering $p_2\left(\sqrt{\frac{\pi}{8}}x\right)$, which turns the problem into a convolution of Gaussians, hence, it has a closed-form solution.

Gerardo Duran-Martin
  • 580