Follow-up: Complete-pooling, no-pooling, and partial-pooling regression in R

Question

This great answer demonstrates the concepts of "complete-pooling regression", "no-pooling regression", and "partial-pooling regression" (3 concepts) using simulated data in R.

However, I wonder how to demonstrate these concepts with this real dataset that reports on math scores (outcome) from $160$ schools (sch.id).

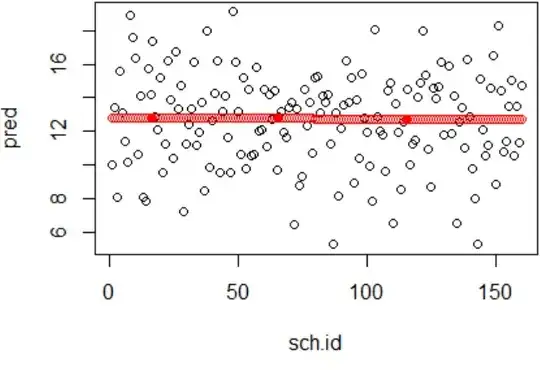
Question: Following this great answer, I thought I should do the following to demonstrate the 3 concepts and expect to see $shrunken$ school means from pred_partial compared to pred_no_pool.

But this is not the case, I wonder what I'm missing?

library(lme4)
library(tidyverse)
library(modelr)
d <- read.csv('https://raw.githubusercontent.com/rnorouzian/e/master/hsb.csv') # Dataset
partial_pooling <- lmer(math~1+ (1|sch.id), data = d)

pred_partial <- data_grid(d, sch.id) %>% add_predictions(partial_pooling) # Predicted Mean Math of Schools
no_pooling <- lm(math~sch.id-1, data = d)
pred_no_pool <- modelr::data_grid(d, sch.id) %>% modelr::add_predictions(no_pooling) # Predicted Mean Math of Schools
plot(pred_partial)            # 'Black' plot of predicted schools means for partial_pooling
points(pred_no_pool, col = 2) # 'Red' plot of predicted schools means for no_pooling

Can you add the output from your code and point out where the problems are? — Demetri Pananos, Jul 08 '20 at 14:18

score 5 · Accepted Answer · answered Jul 08 '20 at 22:15

Here are the no-pooling and partial pooling estimates for each school plotted against one another

Note that the partially pooled estimates are pooled towards the completely pooled estimates (in red). This is the demonstration of the partially pooled estimates being shrunk towards the population mean.

Here is the code to reproduce this figure

library(tidyverse)
library(lme4)
library(modelr)
d <- read.csv('https://raw.githubusercontent.com/rnorouzian/e/master/hsb.csv') %>% 
     mutate(sch.id = factor(sch.id))
complete_pool = lm(math ~ 1, data = d)
no_pool = lm(math~sch.id -1, data = d)
partial_pool = lmer(math ~ 1 + (1|sch.id), data = d)
data_grid(d, sch.id) %>% 
  add_predictions(no_pool, var='no_pooling') %>% 
  add_predictions(partial_pool, var='partial_pooling') %>% 
  ggplot(aes(no_pooling, partial_pooling))+
  geom_point()+
  geom_abline()+
  theme(aspect.ratio = 1)+
  geom_hline(aes(yintercept = mean(d$math)), color = 'red')

score 4 · Answer 2 · answered Jul 08 '20 at 21:35

The problem is that sch.id is stored as an integer (see str(d)) and in order for it to work as intended for the no pooling model, it needs to be treated as a factor variable. You can do this either by mutating the variable into a factor variable using dplyr or simply declaring it as a factor variable in your lm model:

no_pooling <- lm(math~as.factor(sch.id)-1, data = d)

Then you get 160 coefficients, corresponding to the mean math score in each school. From there, you can re-graph to see how much pooling is going on.

@rnorouzian It really should be a factor variable, but lmer might convert it to a factor. I'm not sure, the documentation would probably say. — Demetri Pananos, Jul 08 '20 at 22:15

Follow-up: Complete-pooling, no-pooling, and partial-pooling regression in R

2 Answers2