2

I'm using GAMs to model ozone as a predictor, and using time , temperature and another pollutant (poll) as covariates. I have 20 years hourly data (large dataset), but I'm using 2 periods of 10 years, since I aim to see how the interaction term temperature-poll changes, as well as the differences between both periods. My main interest is to model ozone as a function of temperature-pollutant and be able to interpret how the interaction is changing (and how it affects ozone). I'm only using summer months (3months), so I am not including seasonal terms , only year to account long-term trends.

So far, I tried to fit different models, but I have serious problems with the residuals correlations, even when using lagged variables. I also tried to use AR1 process within the model, which seem not to improve it, but I'm probably missing something here, so I'd really appreciate any suggestion about it. I have read similar posts, but I'm still struggling to find the proper way to model this.

These are the models I tried:

m0 <- <- gam(o3 ~  s(year) + te(temp,poll), data=mydata)

I also fitted some previous models to test the significance of the interaction temp, poll, which is always very significant as expected.

The plots I got from this:

par(mfrow=c(1,2))
acf(residuals(m0))
pacf(residuals(m0))

enter image description here

Model with lag (previous hour of O3)

 m1l <-gam(o3 ~  s(year) + lag + te(temp, poll), data=mydata)

which gives me:

enter image description here

still, autocorrelation problems.

Introducing AR1 process (since usually the concentrations depends also on the previous (time) concentrations. 

m1.cor <- gamm(o3 ~  s(year)  + te(temp, poll), data=mydata,
               correlation = corARMA(form = ~ 1|H, p = 1))

But, still:

enter image description here

When plotting normalized residuals as:

  acf(resid(m1.cor$lme, type = "normalized"))
  pacf(resid(m1.cor$lme, type = "normalized"))

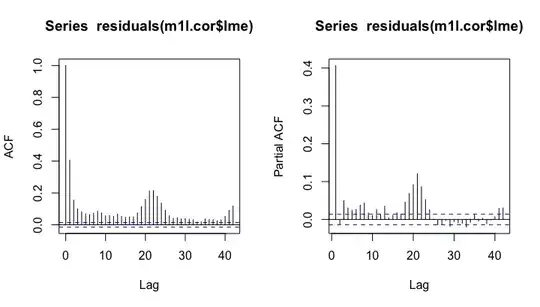
I got the following patterns: enter image description here

Then, I included also the lag in:

m1l.cor <- gamm(o3 ~  s(year)  + lag + te(temp, poll), data=mydata,
               correlation = corARMA(form = ~ 1|H, p = 1))

enter image description here

With normalized residuals:

enter image description here

I still see some problems, and I don't know how to improve the models.

I'm probably missing something here, and I might use another term or the autocorrelation should be handled in a different way. Then, I'd appreciate any suggestion or comment about it.

user3231352
  • 171

1 Answers1

2

For the gamm() models, you need to pass acf() and pacf() the normalized residuals to have them take into account the correlation structure of the model.

Use

resid(m1.cor, type = "normalized")

and

resid(m1l.cor, type = "normalized")

to get these normalized residuals for each of the two models.

Gavin Simpson
  • 47,626
  • Thanks a lot for your comment @Gavin. I just edited my question, adding the plots using normalised residuals. Unfortunately I didn't see too much improvement, so I'm still a bit lost here. Hope to get some feedback about it. Thanks again! – user3231352 Oct 31 '19 at 19:49