If A is a binary faction (1 A and 0 not A) and if the odds ratios of A to B is (say) 1.2409 (24 percent or e ^ 0.2158). Then is the odds ratio of B to A 76% or 1 – 0.24?
Asked
Active
Viewed 103 times
2
-
the odds ratio of B to A = 1/1.0249. – user158565 Jul 28 '19 at 16:41
-
I constantly mix odds and odds ratio up. I ended up creating a confusion table like the one below. – Jeff Jul 28 '19 at 19:17
-
Definition of OR of A to B: $OR_{AB} = \frac {P(A=1)/(1-P(A=1))} {P(B=1)/(1-P(B=1))}$. Definition of OR of B to A: $OR_{BA} = \frac {P(B=1)/(1-P(B=1))}{P(A=1)/(1-P(A=1))}$. So $OR_{BA} = 1/OR_{AB}$ – user158565 Jul 28 '19 at 19:26
1 Answers
1
Neither, maybe you are confused with odds and odds-ratios. But odds and odd ratios are two different things.
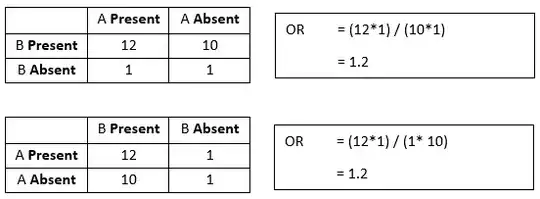
The odds ratio is defined as the ratio of the odds of A in the presence of B and the odds of A in the absence of B. Or equivalently (due to symmetry), the ratio of the odds of B in the presence of A and the odds of B in the absence of A.
Given your example, you could construct the following 2x2 table:
Therefore, if the odds ratio of A to B is 1.2409 to 1, then the odds ratio of B to A is 1.2409 to 1 too.
Justin Lange
- 432
- 4
- 7