First, I'll start with some background that may explain the ignorance that will likely be encountered in the remainder of the post. I am an archaeologist attempting to study the flexural strength of specific types of stone before and after thermal alteration. I have no mechanical engineering training and only limited statistical training. What little knowledge I do possess is essentially autodidactic. Also, this will be a lengthy post.
For this experiment I loosely followed the ASTM testing standard for characterizing the flexural strength of advanced ceramics at ambient temperature. This ASTM standard calls for the use of Weibull stats to characterize the flexural strength of a given ceramic and specifies a minimum of 10 observations for calculating the mean. The testing procedure is designed to obtain strength data, rather than time to failure data.
My goal is to test for any significance in the Weibull moduli and/or characteristic strengths between my raw and thermally altered sample groups. I have calculated both of these statistics by following a video (https://www.youtube.com/watch?v=dMOUlCOcP2U&t=1s) I ran across on YouTube. Here are some example data, followed by my procedures and results. The strength data indicate the flexural strength of individual specimens, measured in megapascals (MPa). Flexural strength is a bulk property, theoretically independent of specimen dimensions.
Example Data:
Calculations:
Here are the data for the Raw sample group after applying the procedures presented in the YouTube video:
Where:
FLEX = Specimen flexural strength
F = (RANK-.5)/n [sorted smallest to largest]
X = LN(FLEX)
Y = LN(LN(1/(1-FLEX)))
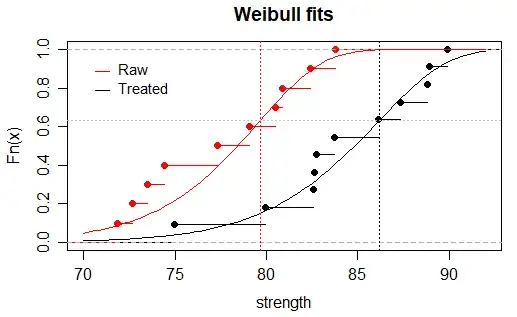
When plotted, the graph looks like this. I ran a linear regression through each of the datasets. As I understand it, the slopes of these regressions indicate the Weibull moduli.
So, the Weibull modulus of the raw group is 20.874, while the treated group is 22.237.
To calculate the characteristic strengths, I did the following:
FLEXc = e^|b/Wm|
Where:
FLEXc = characteristic strength
b = intercept of linear regression
Wm = Weibull modulus
Using this formula, the resulting characteristic strength of the raw sample group is 79.609 MPa, while the treated group is 86.351 MPa.
My overarching question:
How can I use these data to meaningfully compare the raw and treated sample groups?