1

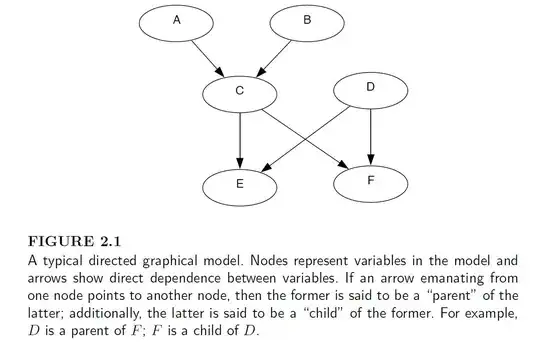
Below is a Directed Acyclic Graph (Fig.a). From this figure, it is said that:

$E$ and $F$ are conditionally independent given $C$ and $D$.

I am confused about it. Let's assume the causal relationships among $A \sim F$ in Fig.a are:

\begin{cases}C=A-B\\E=C+D\\F=C\times D\end{cases}

Then if we know the value of $C$ and $D$, $E$ and $F$ are determined. In addtion, since the equation can be written as: $E=D/F+D$, then $E$ and $F$ are dependent given $D$.

Why they are conditionally independent given $C$ and $D$?

I find that in this post, a paper from Elwert F. and Winship C. (2014) is recommended. I read it (though not fully understand), and think that the relationship among $C, D, E, F$ is a combination of Figure 3 & 4 (attached below as Fig.b) in their paper:

  • from the view of Figure 3, $E$ and $F$ are associated by common cause (i.e., $C$ and $D$);
  • from the view of Figure 4, $E$ is the collider of $C$ and $D$; $F$ is the collider of $C$ and $D$.

Fig.a Fig.b

Noah
  • 33,180
  • 3
  • 47
  • 105
T X
  • 1,027
  • Your question seems to come down to "why are two constants independent?" Although intuition may be of little help, it's a simple matter to apply the definition of independence to verify this is the case. – whuber Jun 25 '19 at 14:36
  • I changed $A$ ~ $F$ to $A \sim F.$ That is standard usage. $\qquad$ – Michael Hardy Jun 25 '19 at 21:39

1 Answers1

2

When two random variables $A$ and $B$ are independent, that means we cannot learn anything about $A$ by observing $B$, or vice versa. Whatever we knew about $A$ before observing $B$, we know nothing more afterwards.

In your graph, $E$ and $F$ are related through common causes. So, in general, observing $E$ can tell us something about what values $F$ is likely to take. More specifically, $E$ gives us information about $C$ and $D$, and from that information we can make guesses about $D$. So $E$ tells us something about $F$ only because it tells us about $C$ and $D$.

But now suppose we actually get to observe $C$ and $D$. We already know their values, so there is nothing more we can learn about them by observing $E$. This means that $E$ now also can tell us nothing more about $F$. $E$ was only informative about $F$ when it could tell us something about $C$ and $D$.

In your example, it is true that you can work out the value of $E$ from $F$. And indeed, if you know $D$ and $F$ but you don't know $C$ (for instance), then you have to rely on $F$ to figure out the value of $E$ (using $E=D/F+D$). But if you're also given $C$, then you can work out $E$ without having to know $F$ (using $E=C+D$). Thus, when $C$ and $D$ are given, there is no more information about $E$ in $F$ that you couldn't already get from $C$ and $D$.

Note also that the statement specifically says that $E$ and $F$ are conditionally independent given both $C$ and $D$. Given only $C$ or $D$, they are still mutually dependent.

Ruben van Bergen
  • 7,539