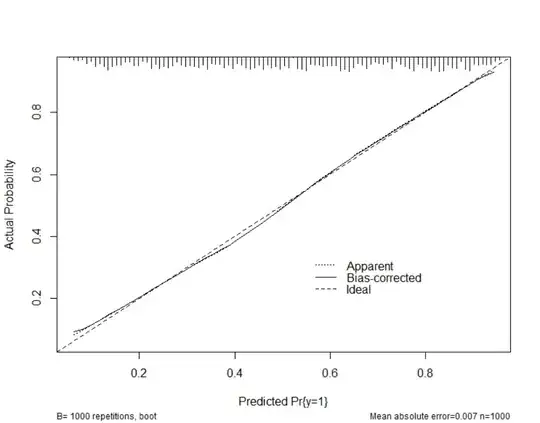
I have a dataset that contains a binary response variable: equal to 1 if the person responded to the survey and 0 otherwise, as well as a host of auxiliary variables X. What I want to do is use this data to estimate response probabilities. To do this I perform cross validation on my data and test various algorithms. Now my issue is that my data is labeled in that I know whether the record responded or not, however it is unsupervised in that I don't know what I truly care about which is the response probability. The question then becomes, can I use the classification accuracy derived from cross validation to infer that my class probabilities are good?
For example, I compare two algorithms A and B. A has classification accuracy 90% and B has classification accuracy 80% can I infer that the class probabilities that A gives are then better than what B gives?
If not what other measure can I use to infer quality?