I'm going to provide a simulated case. However, the question is of a general nature (see end of the post). Let's suppose we have some data generated in this way:
set.seed(123)
n <- 10000
x <- rpois(n, 2)
x2 <- rpois(n, 2)
dat <- data.frame("Dependent"= x + rpois(n, 1), "Independent"= x)
newDat <- data.frame("Independent" = x2, "Dependent"= x2 + rpois(n, 1))
If we were seeing this data for the first time, we would do some EDA and conclude that a closely approximating distribution could be a Poisson:
hist(dat$Dependent, main = "Histogram of response", xlab = "Dependent")
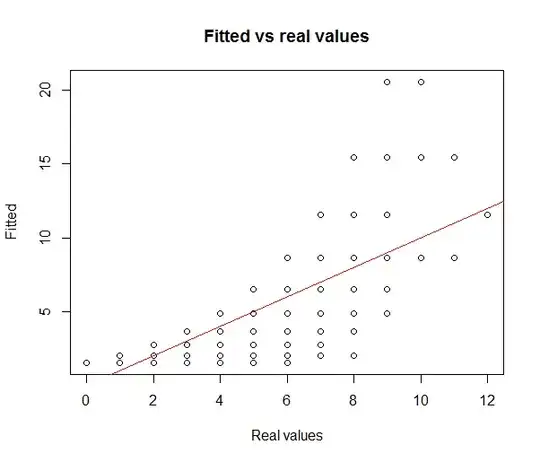
Hence, we fit a glm with Poisson process and check the fit and Pearson residuals:
plot(dat$Dependent, fitted(glmPoisson), main="Fitted vs real values", xlab="Real values", ylab = "Fitted")
abline(0,1, col="red")
plot(fitted(glmPoisson), residuals(glmPoisson, type = "pearson"), main="Fitted vs Pearson residuals", ylab="Pearson residuals", xlab = "Fitted")
From these simple plots, we clearly see that the fit is awful and residuals are clearly showing a pattern. Also, it is not able to model unseen data by the same process:
However, if we run the same analysis assuming an underlying Gaussian process, all these problems disappear and the fit/predictive power is excellent:
glmGaussian <- glm(Dependent ~ Independent, data = dat, family = gaussian)
summary(glmGaussian)
plot(dat$Dependent, fitted(glmGaussian), main="Fitted vs real values", xlab="Real values", ylab = "Fitted")
abline(0,1, col="red")
plot(fitted(glmGaussian), residuals(glmGaussian, type = "pearson"), main="Fitted vs Pearson residuals", ylab="Pearson residuals", xlab = "Fitted")
plot(newDat$Independent, predict(glmGaussian, type = "response", newdata = newDat), main = "New actual values vs predictions", xlab = "New values", ylab = "Predictions")
abline(0,1, col="red")
Hence:
- Why, even if the underlying process is Poisson, the model is better when Gaussian?
- In general, how can one decide a-priori the functional process, given that even in this simulated case we would have got the model completely wrong?