Why does a t-test on similar random samples often come out with a small p-value?

Question

Running the following Python code, I often get very small p-values, sometimes even around 0.01.

a, b = np.random.normal(0,1,100000), np.random.normal(0,1,100000)
ttest_ind(a,b).pvalue

As the mean and std are the same and my sample size is pretty large, I'd expect getting p-values that are far away from zero.

Here is a histogram of the p-values I'm getting:

Why does this happen?

That's a seriously wrong histogram if in fact it represents a large number p-values from tests of the null distribution! It should look nearly flat and horizontal: see https://stats.stackexchange.com/search?q=p-value+uniform. How many tests does it reflect? — whuber, Feb 16 '19 at 22:35
It looks pretty uniform to me -- just with a lot of bins relative to the number of observations; looks like 100 bins, so with the average looking close to 10, presumably the count in each bin would be binomial(1000,0.01) (which I admit is odd given the larger number the code indicates). The histogram looks reasonably consistent with that binomial (perhaps also with some allowance for some program-choice of bin origin and width based on the sample). — Glen_b, Feb 16 '19 at 23:41
@Michael If H0 is true, what is the probability that $p\leq\alpha$ for any $\alpha$? (i.e. what is the probability of a type I error?). As whuber indicates many posts on site discuss this issue. — Glen_b, Feb 16 '19 at 23:50

score 6 · Accepted Answer · edited Feb 17 '19 at 12:06

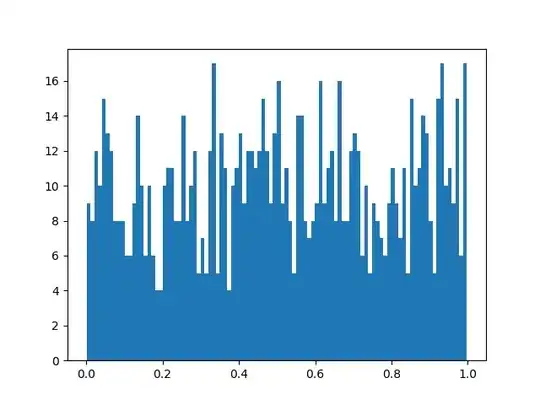
I used R with your setup and generated 300 p-values from a t-test under the same setting you used. Here is the histogram of the p-values:

Here is the quantile-quantile plot which depicts the quantiles of the p-value distribution against uniform quantiles:

As expected, the distribution of the p-values looks uniform.

Finally, here are the p-values plotted against their index:

As you can see in this last plot, the p-values can be pretty much anything in the range 0 to 1.

In fact, as explained by Geoff Cumming in his fabulous video Dance of the p-values, when you replicate a study under similar conditions many times, you can't really use the p-value from the current replication to tell you something about the expected magnitude of the p-value from the next replication because the p-value from the current replication is simply not very informative that way - it gives extremely vague information about the
p-value from the next replication.

Towards the end of the video, Geoff Cumming lists 80% prediction intervals where you can expect the p-value from the next replication to be found when you know the p-value from the current replication. In particular:

P-value from current replication          80% Prediction interval for p-value for next replication

        0.05                                         0.00008 to 0.44

The video goes into more depth so watching it is worthwhile: https://youtu.be/5OL1RqHrZQ8.

If you wanted to see the R code I used, here it is:

set.seed(101)

p.value <- NULL

for (i in 1:300){

   a <- rnorm(100000, 0, 1)

   b <- rnorm(100000, 0, 1)

   t <- t.test(a,b, var.equal=TRUE)

   p.value <- c(p.value, t$p.value)

}

require(MASS)

truehist(p.value)

require(car)

qqPlot(p.value, distribution = "unif")

plot(p.value, type="h", col="dodgerblue")

If you use larger bin widths for your histogram, you should get a nicer looking histogram. The bin width you are currently using seems far too small.

Why does a t-test on similar random samples often come out with a small p-value?

1 Answers1