0

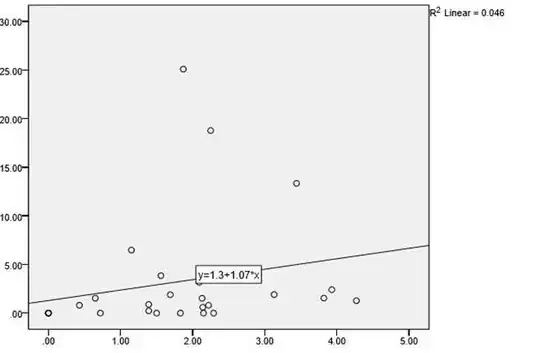
I am correlating two small sets of values – 28 items each. The data are normally distributed and Pearson‘s test shows a weak, non-significant correlation. On the other hand, Spearman’s test shows a moderate and statistically significant correlation. Can I say there is a moderate correlation among two sets?

The scatter plot follows. Sorry for my mistake.

enter image description here

Glen_b
  • 282,281
H12345
  • 3
  • Spearman and Pearson's indices are based on different informations extracted from the data. The former is based on ranks, hence they are not measuring the same thing. Since your data are normally distributed, maybe Pearson would make more sense. – utobi Jan 16 '19 at 12:16
  • 1
    The information you give, which concerns your ability to detect nonzero correlation, is nearly irrelevant to the question you ask, which concerns how much correlation there is. Why not report the correlation in the data, provide an assessment of the uncertainty in it (such as a confidence interval if the data are a random sample), and leave it at that? Your audience will be better served by such an analysis. You can call it "moderate" if you like, but such non-quantitative terms are rarely useful. – whuber Jan 16 '19 at 13:33
  • @utobi if the relationship is not linear -- marginal normality or not - then the Pearson correlation will only pick up part of it at best. $\quad $ H12345: As a reader of a paper my personal questions about a relationship would mostly be answered by a plot more than by a correlation coefficient, and even less by a p-value – Glen_b Jan 17 '19 at 04:43
  • I have edited the plot you posted into your question – Glen_b Jan 17 '19 at 04:48
  • @Glen_b as far as I can see the OP's question is about correlation, hence about non-directional association between two variables. Certainly regression would be an option, but then you have to specify which is the response and which is the predictor... – utobi Jan 17 '19 at 09:09
  • Sorry, I don't understand how this relates to the point; I was responding to your statement "Since your data are normally distributed, maybe Pearson would make more sense"; I don't see how normality is particularly relevant to what the Pearson correlation measures, which is linear correlation – Glen_b Jan 17 '19 at 09:24
  • "Since your data are normally distributed, maybe Pearson would make more sense" is to say that from a pure estimation perspective and under (joint) normality, Person is asymptotically unbiased and fully efficient, being it the maxim likelihood estimator. Now if the true relation is not linear, I doubt Spearman would do much better than Pearson any way. – utobi Jan 17 '19 at 12:32

1 Answers1

0

You can say there is a moderate Spearman correlation. However, when this sort of thing happens, it is a good idea to find out why. I would look at a scatterplot of the data and probably add a smooth or more; one nicely enhanced scatterplot (if I say so myself!) is the one I created for a presentation on scatterplots. I used SAS but it could be done in R or another package.

enter image description here

Glen_b
  • 282,281
Peter Flom
  • 119,535
  • 36
  • 175
  • 383