0

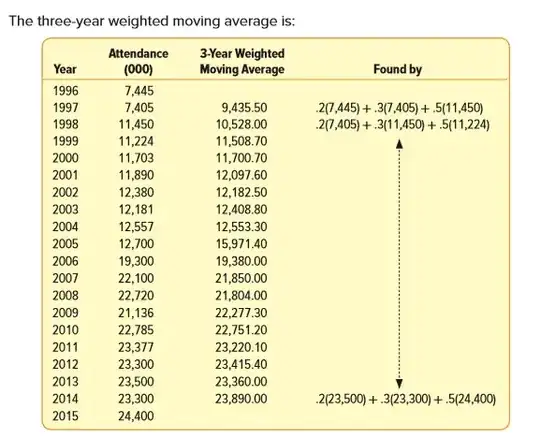
I have two questions about moving average calculation in Python vs moving average example in a textbook.

  1. The task is to calculate a three-year moving average. In Python, I am using

    df['moving_average'] = df['production'].rolling(window = 3).mean()

and get the following results:

enter image description here

I don't understand why in the textbook, they start with the middle year i.e. not from 2000 but 1999? enter image description here

  1. In the textbook, they say, 'Four-year, six-year, and other even-numbered-year moving averages present one minor problem regarding the centering of the moving totals and moving averages. Note in Table 18–3 below there is no center time period, so the moving totals are positioned between two time periods. The total for the first 4 years (42) is positioned between 2009 and 2010. The total for the next 4 years is 43. The averages of the first four years and the second 4 years (10.50 and 10.75, respectively) are averaged, and the resulting figure is centered on 2010. This procedure is repeated until all possible four year averages are computed.' And get the following results: enter image description here

However, if you do it in Python, using the above function, you will get: enter image description here

Their logic seems to make sense. Does it mean that the function in Python is just simplification and to get more accurate results, I need to develop a formula myself? And the question still remains why they start with the 3rd year.

  1. Calculation of weighted moving average enter image description here
Ekaterina Ponkratova
  • 25
  • Hi Nick, I wonder why did you edit the question by removing greetings and two more words? Since when is it unacceptable and the site became a Grammar checker? – Ekaterina Ponkratova Dec 01 '18 at 10:36
  • Look around you. We want concise, precise technical questions without extra fuss. See e.g. https://stats.meta.stackexchange.com/questions/1992/whats-the-site-policy-on-removing-text-such-as-thank-you-or-this-question-i for discussion. – Nick Cox Dec 01 '18 at 10:48

1 Answers1

2

It is a good principle to give a precise reference, not "a textbook" or "the textbook". In this thread we don't much care which textbook it is, as the issues are standard, but often it is important to know which it is.

The methods are all the same in essence. There is one choice for all windows, whether with odd or even numbers of values, and a second choice for windows with even numbers.

In all cases, the difference is just whether you are thinking of the moving average for $x$ at times $t$ as (for example) $(x_{t -1} + x_t + x_{t+1})/3$ or as $(x_{t -2} + x_{t-1} + x_t)/3$. Indeed, in principle you could write $(x_{t} + x_{t+1} + x_{t +2})/3$.

Depending on how you think of your moving averages, you can align results with different positions in the series.

In practice one knows past values and possibly the present value, but future values are unknown.

For windows with even numbers of values, textbook writers can place results "between the lines", but in arrays as processed by all programming, mathematical and statistical languages I know about you must place results into arrays with integer indexes.

Nick Cox
  • 56,404
  • 8
  • 127
  • 185
  • Thank you, Nick. 'Depending on how you think of your moving averages, you can align results with different positions in the series.' is a good answer but broad answer. How do I know what to think of my moving average? Is it something that once I decide on, I would stick to it? Or I need to try different options checking where the diff between the actual and predicted values is minized? – Ekaterina Ponkratova Dec 01 '18 at 11:01
  • I don't know how you think of your moving average either, but it all hinges on what you're trying to do. If I am smoothing 19th century, the moving average for 1880 can use any vbalue for 1881 on because we know that too. In predicting future sales from past sales, or some such, only past values are known. So what is known and why are you doing this are the questions you need to ask. If the calculation is in real time, there is no choice to be made. – Nick Cox Dec 01 '18 at 11:11
  • 'what is known and why are you doing this are the questions you need to ask' – Ekaterina Ponkratova Dec 01 '18 at 11:22
  • We lack a context on what you're trying to do. If it's prediction, then a moving average with equal weights is not especially suitable. – Nick Cox Dec 01 '18 at 11:30
  • I was checking literature on moving average while coding in Python and I realized that my results are different from the textbook results. So, the above Python function calculates xt + 1 results as (xt−2+xt−1+xt)/3 and if I have a different case, I need to write the function myself. Clear. – Ekaterina Ponkratova Dec 01 '18 at 11:36
  • Nick, just another question about weights as you brought them up, I added a screenshot to the original thread. Why do they apply weights in this way? For me, it would make sense to weight up all recent periods with a higher weight than the earlier periods. Why do they use a weighted moving average like that? The task was to ' Compute a three-year moving average and a three-year weighted moving average with weights of 0.2, 0.3, and 0.5 for successive years.' Does it make sense to calculate it with weights for successive years? – Ekaterina Ponkratova Dec 01 '18 at 11:39
  • I guess it depends 'on how you think of your moving averages'. And again, we got to the use case. – Ekaterina Ponkratova Dec 01 '18 at 11:55
  • Again, you're referring to an anonymous text I don't know. If the authors don't explain well, perhaps you need a better text. Different weights can make sense. I don't know a specific justification for 0.2 0.3 0.5 beyond some judgement possibly based on experience. Exponentially weighted moving averages make the notion more systematic. I doubt that you need to write any new code. Python must have functionality for translating vectors so that you copy leading or lagging values of existing vectors, but -- sorry -- I have never used Python and questions on coding issues are off-topic here. – Nick Cox Dec 02 '18 at 09:05