0

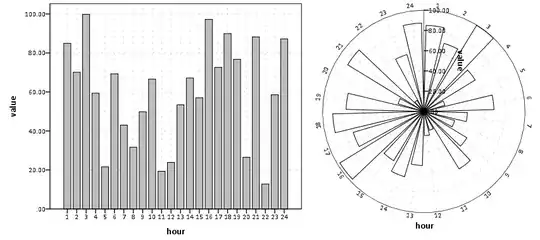
Imagine we have a set of data, with two variables, the first of which can be represented in polar co-ordinates (for example hour or day, or day of week). The second variable is a real valued and has some relationship with the first. The data might look something like the following:

enter image description here

I would like to fit a closed curve to this data, which maximises the likelihood of the data for the purpose of making predictions. I only have a single cycle of data, so I cannot do extract seasonal or trends through decomposition . What methods are recommended?

(p.s. I'm using R)

whuber
  • 322,774
Jinglesting
  • 306
  • 2
    For fitting likelihoods, there's nothing special about this problem. Nothing differs in the least from fitting curves in Cartesian coordinates: as always, you write down the likelihood function and find its maxima. What, then, are you trying to ask? – whuber Oct 28 '17 at 17:36
  • I suppose there is an implicit expectation that since I want the curve to be closed, that I will need to use some other method to generate the curve. I only have experience fitting polynomials. Perhaps my question is, "what is a good basis function for this kind or problem?"... – Jinglesting Oct 28 '17 at 18:00
  • 1
    I was wondering whether that's where you were headed. If you want an answer that has a good chance of being appropriate for your data, then you ought to describe what your data mean and your assumptions about them. Otherwise, you're not really asking about maximum likelihood: your question seems to reduce to "what are ways to fit a continuous function to circular data?" Would that be a correct interpretation? If that's the case, check out https://stats.stackexchange.com/questions/68403/smooth-a-circular-periodic-time-series/68504#68504. – whuber Oct 28 '17 at 20:29

0 Answers0