Plotting non-parametric (E)CDF confidence envelopes for comparison

Question

I have previously asked about a way to test whether two samples are drawn from the same distribution (Non-parametric test if two samples are drawn from the same distribution). I was very glad to learn about the Kolmogorov–Smirnov test. This seems excellent for hypothesis testing with p-values.

I am interested in generalizing this to a visual comparison of samples using confidence bands. I wonder if my idea is valid and, if so, how I can implement it with R, and if not, what a better approach might be.

The idea is to visually plot CDF confidence bands for each of N samples. This should show two things. First, the "tightness" of the confidence bands will suggest how adequate the sample sizes are for drawing inferences. Second, anywhere the confidence bands for a pair of samples do not overlap will indicate a significant difference in the KS-statistic, i.e. a point where one CDF seems to be "greater than" or "less than" another.

Does this make sense? I was hoping to find an example graph on Google Images, but the nearest I found is only one sample:

My graph would be similar, except I would show N samples and look for blank spaces between the confidence bands.

If indeed this sounds reasonable, then I have a few specific questions:

• Is this a well-known technique? (Reference to a description?)
• How should I compute the CDF confidence bands? (Is there an R package that I should use?)
• How valid is the visual comparison of confidence bands? (If I plot two samples, how closely will a non-overlapping point correspond with a significant result from the KS test?)
• What pitfalls should I consider when comparing more than two samples? (Should I adjust the parameters of my confidence bands in the spirit of the Bonferroni correction?) Note: I am okay with the comparison being more informal than a p-value.

Thanks!

UPDATE

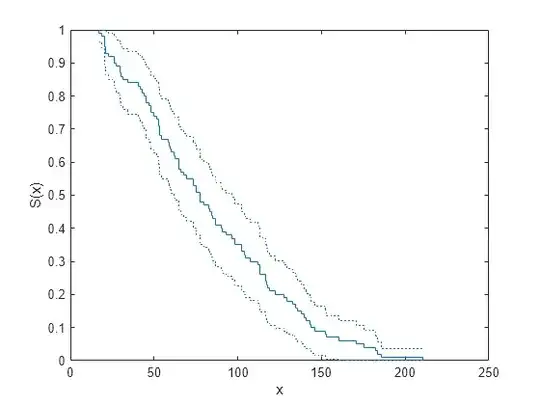
I found an example of the kind of graph that I have in mind now:

I will try to work out how to create such a graphic using ggplot2 and the ecdf.ksCI() function recommended in the comment.

UPDATE 2

Thank you for the answer below. I was able to generate my graph, and here is a sample. I am pleased!

Answer 1

You can use the Kolmogorov-Smirnov test, and invert it to get a confidence band. Let $X_1, X_2, \dotsc, X_n$ be iid observations from some continuous distribution function $F$. Then the KS test statistic is given by $$ D_n = \sup_x \mid \hat{F}_ n(x)-F_0(x) \mid = \max_{i=1,2,\dotsc,n} \max \{\frac{i}{n}-F_0(x_{(i)}),F_0(x_{(i)})-\frac{i-1}{n} \} $$ where $x_{(1)} \le \dotso \le x_{(n)}$ is the order statistics. What is remarkable is that the distribution of $D_n$ do not depend on the assumed null distribution $F_0$ (which must be prespecified). Now we can invert this hypothesis test to get a confidence band. WE can calculate $$ P_{F_0}(D_n \le d) = P_{F_0}( \sup_x \mid \hat{F}_ n(x)-F_0(x) \mid \le d) = \\ P_{F_0}( \hat{F}_n(x)-d \le F_0(x) \le \hat{F}_n(x)+d, \quad \text{for all $x$}) $$ this calculation shows that this is indeed a simultaneous confidence band, valid simultaneously for all $x$.

An implementation of this can be found in the R package (on CRAN) sfsmisc, in the function ecdf.ksCI. (Disclaimer: That was originally my code). An example:

R code:

library(sfsmisc)
set.seed(7*11*13)
ecdf.ksCI( rchisq(50,3), main="ECDF, sample from chisq with 3 df")