20

On the wikipedia page of convolutional neural networks, it is stated that rectified linear units are applied to increase the non-linearity of the decision function and of the overall network: https://en.wikipedia.org/wiki/Convolutional_neural_network#ReLU_layer

Why is increasing non-linearity desired? What effect does it have on the overall performance of the model?

6 Answers6

28

That part of the Wikipedia article leaves a bit to be desired. Let's separate two aspects:

The need for nonlinear activation functions

It's obvious that a feedforward neural network with linear activation functions and $n$ layers each having $m$ hidden units (linear neural network, for brevity) is equivalent to a linear neural network without hidden layers. Proof:

$$ y = h(\mathbf{x})=\mathbf{b}_n+W_n(\mathbf{b}_{n-1}+W_{n-1}(\dots (\mathbf{b}_1+W_1 \mathbf{x})\dots))=\mathbf{b}_n+W_n\mathbf{b}_{n-1}+W_nW_{n-1}\mathbf{b}_{n-2}+\dots+W_nW_{n-1}\dots W_1\mathbf{x}=\mathbf{b}'+W'\mathbf{x}$$

Thus it's clear that adding layers ("going deep") doesn't increase the approximation power of a linear neural network at all, unlike for nonlinear neural network.

Also, nonlinear activation functions are needed for the universal approximation theorem for neural networks to be valid. This theorem states that under certain conditions, for any continuous function $f:[0,1]^d\to\mathbb{R}$ and any $\epsilon>0$, there exist a neural network with one hidden layer and a sufficiently large number of hidden units $m$ which approximates $f$ on $[0,1]^d$ uniformly to within $\epsilon$. One of the conditions for the universal approximation theorem to be valid is that the neural network is a composition of nonlinear activation functions: if only linear functions are used, the theorem is not valid anymore. Thus we know that there exist some continuous functions over hypercubes which we just can't approximate accurately with linear neural networks.

You can see the limits of linear neural networks in practice, thanks to the Tensorflow playground. I built a 4 hidden layers linear neural network for classification. As you can see, no matter how many layers you use, the linear neural network can only find linear separation boundaries, since it's equivalent to a linear neural network without hidden layers, i.e., to a linear classifier.

The need for ReLU

The activation function $h(s)=\max(0,cs)$ is not used because "it increases the nonlinearity of the decision function": whatever that may mean, ReLU is no more nonlinear than $\tanh$, sigmoid, etc. The actual reason why it's used is that, when stacking more and more layers in a CNN, it has been empirically observed that a CNN with ReLU is much easier and faster to train than a CNN with $\tanh$ (the situation with a sigmoid is even worse). Why is it so? There are two theories currently:

  • $\tanh(s)$ has the vanishing gradient problem. As the independent variable $s$ goes to $\pm \infty$, the derivative of $\tanh(s)$ goes to 0:

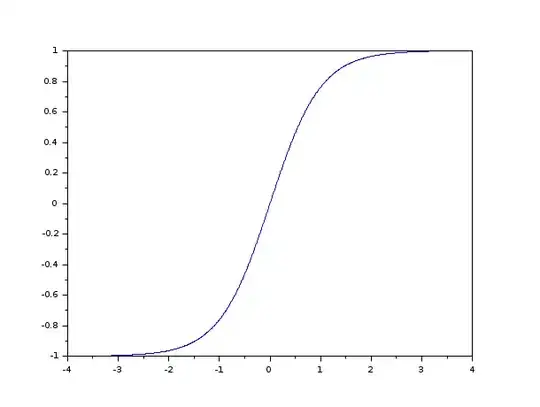
enter image description here

This means that as more layers are stacked, the gradients get smaller and smaller. Since the step in weight space of the backpropagation algorithm is proportional to the magnitude of the gradient, vanishing gradients mean that the neural network cannot be trained anymore. This manifests itself in training times which increase exponentially with the increase in the number of layers. On the contrary, the derivative of ReLU is constant (equal to $c$) if $s>0$, no matter how many layers we stack (it's also equal to 0 if $s<0$ which leads to the dead neurons issue, but this is another problem).

  • there are theorems which guarantee that local minima, under certain conditions, are global minima (see here). Some of the assumptions of these theorems don't hold if the activation function is a $\tanh$ or sigmoid, but they hold if the activation function is a ReLU.
DeltaIV
  • 17,954
  • 3
    +1 for "since it's equivalent to a linear neural network without hidden layers, i.e., to a linear classifier." as a beautiful summary of the proof above – 3yanlis1bos Sep 10 '19 at 01:56
11

I'll give you a very loose analogy (emphasis is important here) that may help you understand the intuition. There's this technical drawing tool, called a French curve, here's an example:

enter image description here

We were trained to use it in high school in a technical drawing class. These days, the same class is taught with CAD software, so you may not have encountered it. See, how to use them in this video.

Here's a straight ruler:

enter image description here
(source: officeworks.com.au)

Can you draw a curved line with a straight ruler? Of course, you can! However, it's more work. Take a look at this video to appreciate the difference.

It's more efficient to use a French curve to draw curved lines than with a straight ruler. You'd have to make a lot of small lines to draft any smooth curve with the latter. enter image description here

enter image description here

It's not exactly the same with machine learning, but this analogy provides you with an intuition why nonlinear activation may work better in many cases: your problems are nonlinear, and having nonlinear pieces can be more efficient when combining them into a solution to nonlinear problems.

Glorfindel
  • 1,118
  • 2
  • 12
  • 18
Aksakal
  • 61,310
  • liked your example +1. but it assumes we want to draw a curve not a line. BTW, do you mind to make the ruler smaller? – Haitao Du Mar 21 '18 at 18:51
  • @hxd1011, for a linear model, a "line", there's no need in ML, a simple linear regression will do – Aksakal Mar 21 '18 at 18:52
  • yes, but many people think linear regression and logistic regression are "machine learning" – Haitao Du Mar 21 '18 at 18:53
  • @hxd1011, they teach both in ML classes, because the layers in ML are very similar to regression in how they turn inputs into outputs. – Aksakal Mar 21 '18 at 18:57
  • 1
    It's a bit more than that. 1) An arbitrarily deep neural network with linear activation functions (also called a linear neural network) is equivalent to a linear neural network without hidden layers. So adding "a lot more layers" ("going deep") doesn't help at all with the approximation power of the linear neural network. – DeltaIV Mar 21 '18 at 19:00
  • Adding neurons ("going wide") helps only so much. The universal approximation theorem of neural networks doesn't hold for linear neural networks, so we know that there exist continuos functions over hypercubes which we will never be able to approximate to the desired accuracy using a linear neural network, no matter how many layers and/or units we add.
    • – DeltaIV Mar 21 '18 at 19:00
  • 2
    +1 I know there will be technical objections to this answer, yet the image is memorable and more than compensates for the fact it's an analogy. – whuber Mar 21 '18 at 19:07
  • I'm not sure about this analogy (or maybe I'm misinterpreting it). It seems to me that the ReLU activation function the OP is asking about is more like using a ruler to approximate a curve with small, straight segments, and less like the French curve (because taking linear combinations and compositions of them as in neural nets gives piecewise linear functions). The important thing then would be the fact that you're allowed to make curves that aren't straight overall, rather than the pieces you compose them out of, no? – user20160 Mar 22 '18 at 09:18
  • @user20160, the fact that ReLU is piece-wise linear is not important in this discussion. what's important is that it's not linear. the fact that it has linear pieces plays a role in terms of computational speed, and subsequently optimization efficiency. – Aksakal Mar 22 '18 at 13:12