Scaling normal $X$ into (0, 1) range whist maintaining distribution shape

Question

Let $X$ be a normally-distributed random variable. How can I transform this $X \in \mathbb{R}$ into another r.v. $Y \in [0; 1]$ whilst maintaining its normal-like shape?

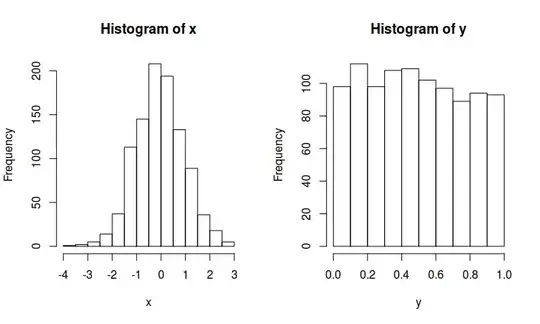
One common way of performing a one-to-one transformation from $\mathbb{R}$ into $[0; 1]$ is to calculate the CDF of the original variable. The "problem" with that approach is that the result will be uniformly-distributed. This is a well-known property, but here is an example to illustrate:

set.seed(2345)
x <- rnorm(1000)
hist(x)
y <- pnorm(x)
hist(y)

The histograms of $x$ and $y$ will look like this:

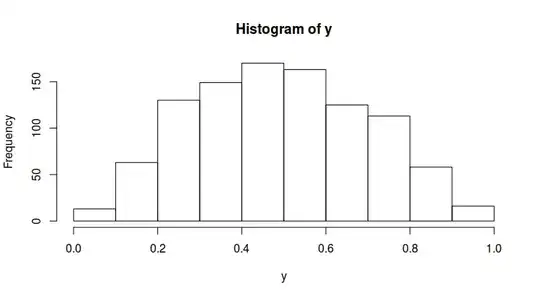
However, as I mentioned, I would like to transform $X \in \mathbb{R}$ into $Y \in [0; 1]$ and have $Y$ bell-shaped?

Answer 1

As you correctly point out, $U=F_X(X)$ will be uniform. Consider now that we have (somehow) identified some sufficiently "normal-like" continuous strictly monotonic distribution function on (0,1) (which we'll call $G$).

Then $Y=G^{-1}(U)$ has distribution $G$. So $Y=G^{-1}(F_X(X))\sim G$

So if we can find some suitable $G$, we're done.

---

Possible distributions with the kind of properties you want:

1. The beta distribution. This is very often used as a distribution for the binomial parameter in Bayesian statistics. If you choose the two parameters to be approximately equal and larger than 2, then you have something that looks roughly normal. The inverse cdf is widely available.

2. A suitably truncated normal. Rescale a normal so that it has mean near the middle of (0,1) and most of its probability in (0,1). For example, $N(\frac12,\frac16^2)$ truncated to the unit interval. The inverse cdf is fairly convenient and (if you don't need the tails of the original distribution) this can avoid the need to go via the uniform.

3. Logit-normal, for some parameter values; to get those, rescale your normal to have a suitable parameter combination such that the logit-normal looks like you want. Typically you'll want $\mu$ not too far from $0$ and $\sigma<1$ (a value like $\frac12$ or $\frac13$ -- or less -- will often be reasonable). Incidentally I think your own answer is a particular case of this with $\sigma=1$. The inverse cdf is quite convenient and this also avoids the need to convert to uniform first.

4. A standard Bates distribution. Take the mean of $k$ independent standard uniforms. The inverse cdf isn't particularly convenient if you're doing this from scratch, but if you can find an existing function to do this (or the related Irwin-Hall, followed by a rescaling), this may be convenient.

5. Raised cosine. Specifically, the one with $f_Y(y) = 1+\cos(\pi(2x-1))\mathbb{I}_{(0,1)}$.

There are many other fairly obvious choices; for example a suitably truncated $t$ would allow you to push up the kurtosis a little (I think all of the previous examples have lower kurtosis than the normal; you may in some circumstances want to get it a bit closer to that of the normal); you could also consider scale mixtures for example.

Answer 2

Thanks to Francis, I ended up doing a simple rescaling of the data in order to achieve what I wanted.

Scaling is achieved by performing the following transformation:

$$ y = \frac{x - \min(x)}{\max(x) - \min(x)} $$

This is a great solution for me because it's fairly shape-constant. No matter how my original variable $X$ looks, $Y$ will be a horizontally-distorted version of it, squished from its original range to $(0, 1)$. This works for me because I had a bell-shaped $X$ which could take any real value and wanted a bell-shaped $Y$ which was $\in (0, 1)$.

---

One drawback of the transformation above for my case was that $\min(x)$ becomes 0 and $\max(x)$ becomes 1 by definition. I wanted $Y$ to be a little more concentrated around 0.5, so the transformation I've actually used was this:

$$ y = \frac{x - [\min(x) - \text{IQR}(x)]}{[\max(x) + \text{IQR}(x)] - [\min(x) - \text{IQR}(x)]} = \frac{x - \min(x) + \text{IQR}(x)}{\max(x) - \min(x) + 2\text{IQR}(x)}, $$ where $\text{IQR}(x) = Q_3(x) - Q_1(x)$ is the interquartile range of $X$.

What happens here is I'm giving the minimum and maximum values extra padding, thus increasing the "range of the observed values of $X$" and, consequently, having the transformed values lay farther from the extremities 0 and 1.

Answer 3

One solution would be to use the CDF of a logistic distribution. In the example:

set.seed(2345)
x <- rnorm(1000)
y <- 1 / (1 + exp(-x))  # assumes mu = 0 and sd = 1 for Y.

This should give the following histogram for $y$:

At first this seems to answer my question, but I welcome other solutions very much, since this transformation may be too similar to another method I am using and comparing.