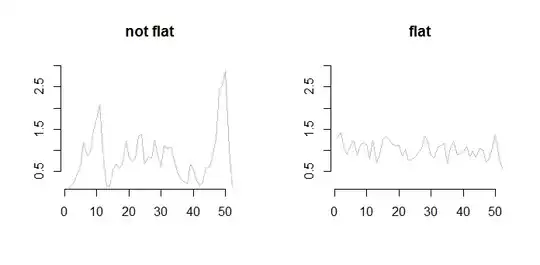
I have multiple short (say, length <100 points) time-series as exemplified below. All the series are made of values measured in the same units. I need to find some criterion for judging their "flatness". Preferably, I'd like to find single numeric value, so that I can find some decision boundary that let's me distinguish the "flat" time-series (second plot) from the "non-flat" ones (first plot).
By "non-flat" time-series I mean the ones that have relatively short periods of significantly increased values. By "flat" time series I mean the ones that have all the time very similar magnitude of changes. Some kind of slight linear trend may, or may not, be present in the series.
Can you suggest something? I tried multiple approaches starting from simple ones (using variance), to more sophisticated ones (using methods for change-point analysis), but without satisfactory results.