16

Are there any non-identical distributions which happen to have the same moment-generating function?

kjetil b halvorsen
  • 77,844

1 Answers1

10

Yes.

In an exercise, Stuart & Ord (Kendall's Advanced Theory of Statistics, 5th Ed., Ex. 3.12) quote a 1918 result of TJ Stieltjes (which apparently appears in his Oeuvres Completes,):

If $f$ is an odd function of period $\frac{1}{2}$, show that

$$\int_0^\infty x^r x^{-\log x} f(\log x) dx = 0$$

for all integral values of $r$. Hence show that the distributions

$$dF = x^{-\log x}(1 - \lambda \sin(4\pi \log x))\ dx, \quad 0 \le x \lt \infty;\quad 0 \le |\lambda| \le 1,$$

have the same moments whatever the value of $\lambda$.

(In the original, $|\lambda|$ appears only as $\lambda$; the restriction on the size of $\lambda$ arises from the requirement to keep all values of the density function $dF$ non-negative.) The exercise is easy to solve via the substitution $x = \exp(y)$ and completing the square. The case $\lambda=0$ is the well-known lognormal distribution.

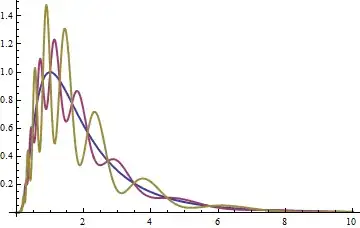
enter image description here

The blue curve corresponds to $\lambda=0$, a lognormal distribution. For the red curve, $\lambda = -1/4$ and for the gold curve, $\lambda = 1/2$.

whuber
  • 322,774
  • 9
    But the lognormal distribution does not have a moment-generating function. – onestop Mar 21 '12 at 16:44
  • 7
    That's an excellent point, onestop, and I have to agree with it. I took the question in the sense of "having the same set of moments" and I should have pointed out that change of interpretation. When the mgf exists as a function (and not just as a formal power series) then it can be inverted to produce a unique density to which it corresponds. – whuber Mar 21 '12 at 16:55
  • Its not true that the lognormal dont have mgf, its only that its not defined on an open interval containing zero – kjetil b halvorsen Apr 21 '17 at 07:10
  • ..... see http://link.springer.com/article/10.1007/s11009-014-9430-7 – kjetil b halvorsen Apr 21 '17 at 08:44
  • 2
    For the record, both @onestop and I were implicitly discussing the existence of an mgf in a neighborhood of $0.$ This sense is often assumed because one of the most basic uses of an mgf is to expand its MacLaurin series (Taylor series around $0$) to compute or analyze the moments and this requires the function to be defined in a neighborhood, not just at $0.$ – whuber Feb 01 '19 at 20:27
  • 1
    @whuber: That's OK, but it seems to be understood implicitely so often that one forgets that mgf's can be useful otherwise too. See also (the links in) https://stats.stackexchange.com/questions/389846/moment-generating-function-for-lognormal-random-variable/390185#390185 – kjetil b halvorsen Feb 02 '19 at 17:59
  • Should for all integral values of $r$ be for all integer values of $r$? If not, what does integral mean in this context? – Richard Hardy Mar 05 '21 at 06:38
  • @Richard "integer values" is poor grammar; "integral values" means "values that are integers." – whuber Mar 05 '21 at 14:37
  • @whuber, thank you. This was beyond my knowledge of English (not a native speaker). – Richard Hardy Mar 05 '21 at 14:45
  • I don't get this at all. The moment generating function is just the Laplace transform of the pdf, and it is a well-known and basic theorem that the Laplace transform of any two functions will be different unless their difference is some function which is zero almost everywhere. How can this result be true then? – Mike Battaglia Jun 09 '22 at 02:22
  • One thought is that the original post is about the moment-generating function being unique, not the moments. The moments are just the derivatives of the moment-generating function, so if this function is analytic, then the moments totally characterize the moment-generating function as the coefficients of the Taylor expansion and are also unique. Is the idea here that this result (non-unique moments) can thus only happen if the function is not complex analytic, and thus some of the derivatives (and thus moments) don't exist? – Mike Battaglia Jun 09 '22 at 02:25
  • @Mike The mgf needn't exist at all (in the sense of a function defined in a neighborhood of $0$). Consider a Pareto distribution, for instance: its tail is heavier than exponential. When the mgf does exist, the focus is not on being Complex analytic but on being Real analytic at the origin only. – whuber Jun 09 '22 at 12:20
  • OK, that makes sense. So if the mgf exists, it must be unique. However, because it's only real-analytic and not complex-analytic, we can have two different mgf's with the same derivatives at the origin. For instance, we could have two piecewise-analytic mgfs which agree on a neighborhood of 0 but then diverge beyond that, and which would thus have the same moments. If I get what you are saying correctly, that is. – Mike Battaglia Jun 10 '22 at 08:38