What are the properties of a half Cauchy distribution?

Question

I am currently working on a problem, where I need to develop a Markov chain Monte Carlo (MCMC) algorithm for a state space model.

To be able to solve the problem, I have been given the following probability of $\tau$: p($\tau$) = 2I($\tau$>0)/(1+$\tau^2$). $\tau$ being the standard deviation of $x$.

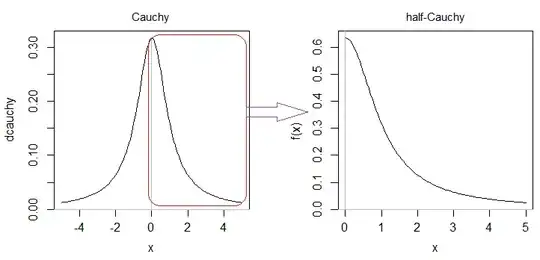
So now I know that it is a half-Cauchy distribution, because I recognise it from seeing examples and, because I was told so. But I do not fully understand why it is a "Half-Cauchy" distribution and which properties come with it.

In terms of properties I am not sure what I want. I am fairly new to this type of econometrics theory. So it is more for me to understand the distribution and how we use in a state space model context. The model itself looks like this: \begin{align} y_t &= x_t + e_t \\ x_{t+1} &= x_t + a_{t+1} \\[10pt] a_{t+1} &\sim ~ N(0, \tau^2) \\ p(\sigma^2) &\propto 1/\sigma^2 \\[3pt] p(\tau) &= \frac{2I(\tau>0)}{\pi(1+\tau^2)} \end{align}

Edit: I included $\pi$ in p($\tau$). Thank you for pointing this out.

Answer 1

A half-Cauchy is one of the symmetric halves of the Cauchy distribution (if unspecified, it is the right half that's intended):

Since the area of the right half of a Cauchy is $\frac12$ the density must then be doubled. Hence the 2 in your pdf (though it's missing a $\frac{1}{\pi}$ as whuber noted in comments).

The half-Cauchy has many properties; some are useful properties we may want in a prior.

A common choice for a prior on a scale parameter is the inverse gamma (not least, because it's conjugate for some familiar cases). When a weakly informative prior is desired, very small parameter values are used. However, there are cases where the posterior is somewhat sensitive to the specific choice so perhaps 'weakly informative' isn't a great description of such a prior.

The half-Cauchy is quite heavy tailed and it, too, may be regarded as fairly weakly informative in some situations. Gelman ([1] for example) advocates for half-t priors (including the half-Cauchy) over the inverse gamma because they have better behavior for small parameter values but only regards it as weakly informative when a large scale parameter is used*. Gelman has focused more on the half-Cauchy in more recent years. The paper by Polson and Scott [2] gives additional reasons for choosing the half-Cauchy in particular.

* your post shows a standard half-Cauchy. Gelman would probably not choose that for a prior. If you have no sense at all of the scale, it corresponds to saying that the scale is as likely to be above 1 as below 1 (which may be what you want) but it wouldn't necessarily fit with some of the things Gelman is arguing for.

[1] A. Gelman (2006),
"Prior distributions for variance parameters in hierarchical models"
Bayesian Analysis, Vol. 1, N. 3, pp. 515–533
http://www.stat.columbia.edu/~gelman/research/published/taumain.pdf

[2] N. G. Polson and J. G. Scott (2012),
"On the Half-Cauchy Prior for a Global Scale Parameter"
Bayesian Analysis, Vol. 7, No. 4, pp. 887-902
https://projecteuclid.org/euclid.ba/1354024466