Using PCA on an image dataset prior to classification with a neural network

Question

I have an image data matrix $X \in \Re^{N \ \text{x}\ p}$ where $N=50000$ is the number of image examples, and $p=3072$ is the number of image pixels: $p = 3072 = 32 \times 32 \times 3$, because each image is a 3-channel $32 \times 32$ image. Furthermore, each of the 50000 images belongs to 1 of 10 possible classes. That is, there are 5000 images of class 'car', 5000 images, of class 'bird', etc... and there are 10 classes total. This is a part of the CIFAR-10 dataset.

The ultimate goal here is to perform classification on this data set. To this end, the professor mentioned to try PCA on this, and then placing those features into a classifier. As my classifier, I am using a fully connected neural network with one hidden layer and a softmax output.

My problem is that I believe I have done PCA in the correct way, but I think my way might possibly be mis-applied.

This is what I have done:

In order to compute the PCA of my data, this is what I did so far:

First, I compute the mean image $\mu \in \Re^{1\text{x} p}$. Let $x_n$ be the $n$'th row of $X$. Then,

$$ \mu = \frac{1}{N} \sum_{n=1}^{N} x_n $$

Compute the covariance matrix $C \in \Re^{p \text{x} p}$ of my image data:

$$ C = \frac{1}{N-1}(X - \mu)^{T}(X - \mu) $$

Perform an eigen-vector decomposition of $C$, yielding $U$, $S$, and $V$, where the matrix $U$ encodes the principal directions (eigenvectors) as columns. (Also, assume that eigen-values are already sorted in decreasing order). Thus:

$$ [U, S, V] = \text{eig}(C) $$

Finally, perform PCA: i.e, compute a new data matrix $P \in \Re^{N \text{x} k}$, where $k$ is the number of principal components we wish to have. Let $U_k \in \Re^{p \text{x} k}$ - that is, a matrix with only the first $k$ columns. Thus:

$$ P = XU_k $$

The Question:

I think my method of performing PCA on this data is mis-applied, because the way I have done it, I basically end up decorrelating my pixels from each other. (Assume I had set $k=p$). That is, the resultant rows of $P$ look more or less like noise. That being the case, my questions are as follows:

• Have I really de-correlated the pixels? That is, have I in fact removed any coupling between pixels that a prospective classifier might have hoped to use?
• If the answer to the above is true, then why would we ever do PCA this way?
• Finally, related to the last point, how would we do dimensionality reduction via PCA on images, if in fact, the method I have used it wrong?

---

EDIT:

After further studying and plenty of feedback, I have refined my question to: If one were to use PCA as a pre-processing step for image classification, is it better:

• Perform classification on the k principal components of the images? (Matrix $X_{new} = X U_k$ in the above, so now each image is of length $k$ instead of the original $p$)
• OR is it better to perform classification on the reconstructed images from k-eigenvectors, (which will then be $X_{new} = X U_k U_k^T$, so even though each each image is STILL the original $p$ in length, it was in fact reconstructed from $k$ eigenvectors).

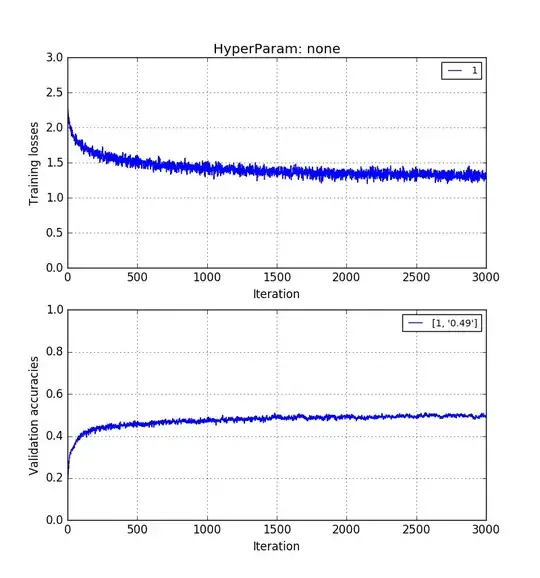
Empirically, I have found that validation accuracy without PCA > validation accuracy with PCA reconstruction > validation accuracy with PCA PCs.

The images below show that in the same order. 0.5 > 0.41 > 0.31 validation accuracies.

Training on raw pixels images of length $p$:

Training on images of length $p$ but reconstructed with k=20 eigenvectors:

And finally, training on the $k=20 principal components themselves*:

All this has been very illuminating. As I have found out, PCA makes no guarantees that the principal components make demarcation between different classes easier. This is because the principal axes computed are axes that merely try to maximize the energy of projection across all images, agnostic to image class. In contrast, actual images - whether faithfully reconstructed or not, still maintain some aspect of spatial differences that can go - or should go - towards making classification possible.

Answer 1

I agree with all @amoeba 's comments. But would add a couple of things.

The reason PCA is used on images is because it works as' feature selection ' : objects span multiple pixels, so correlated changes over multiple pixels are indicative of objects. Throwing away un correlated Pixel changes is getting rid of' noise' which could lead to bad generalisation.

In general nns (using gradient descent) do better with sphered inputs (ie un correlated normalised inputs), this is because then your error surface will be more symmetrical and so the single learning rate works better (you need a small learning rate in highly curved directions and a large learning rate in shallow directions).

Did you normalise your inputs (good) as well or just decorrelate?

Did you use l2 regularisation? This has a similar effect to PCA regularisation. For correlated inputs it emphasises small similar weights (ie averaging out the noise, penalising large weights so single pixels cannot have a disproportionate effect on classification) (see eg elements of statistical learning book), so perhaps you saw no benefit to PCA because the l2 regularisation was already effective. Or perhaps the nn was too small to overfit.

Lastly did you reoptimise the parameters... I would expect you would need different learning rate and other parameters after changing to first k principal components.

Answer 2

Per definition, PCA removes correlation among variables. It is used before classification because not all classifiers can deal well with high dimensional data (but neural nets can) and not all classifiers can deal well with correlated variables (but neural nets can). Especially with images, you typically do not want to remove correlation and you also want multiple layers such that neighboring pixels can be aggregated into image features. Your experimental results reflect the poor choice of this technique for this particular task.

Answer 3

If your images(the images that you vectorized so that each image is now a single row with M columns where M is the number of total pixels x 32 x 32 x 3) contains little to no correlation, then the number of principle components required to explain most of the variances(>95% for example) in your data increases. In order to determine how "feasible" PCA is, checking explained variance is a good idea. In your case, since your data matrix has a size of NxM where M > N, maximum number of components is N. If the number of PCs required is close to 50000, then using PCA makes no sense. You can calculate the explained variance by:

explained variance = 
sum of the eigenvalues that correspond to the PCs you use / 
sum of ALL eigenvalues

I would choose the number of principle components which explains at least more than 90% variance. Another method for choosing the correct number of PCs is drawing the number of PCs vs. explained cumulative variance plot. In the plot you may choose the number where the explained variance doesn't increase significanly anymore.

Thus, I think your problem might be choosing a good number of PCs.

Another problem might be related to projection of the test samples. When you divided your samples for constructing the NN and for testing the NN, you need to project the test data set using the eigenvectors obtained from the training data set.