sampling from a mixture of two Gamma distributions

Question

Assuming that all the mixture parameters are known, how can one sample from a mixture of $\texttt{Gamma}(\alpha,\beta)$ distributions: $$\theta \sim \pi \texttt{Gamma}(\alpha_1,\beta_1)+(1-\pi)\texttt{Gamma}(\alpha_2,\beta_2)$$ Is it done by sampling a whole bunch of $\theta$s from either of the distributions and putting them in a pool and at the end computing their corresponding probability according to the mixture, and then sampling proportional to the accumulated computed probabilities?

Answer 1

Actually, it is much simpler. Assuming that you have $K$-component mixture of gamma distributions the algorithm to draw sample of size $N$ is as follows:

Repeat $N$ times:
1. draw $k$ from categorical distribution parametrized by vector $\pi$,
2. draw single value from $k$-th gamma distribution parametrized by $\alpha_k$, $\beta_k$.

You can use similar algorithm to draw samples from mixture of any distributions. Notice that this follows exactly from the definition of mixture distribution:

mixture distribution is the probability distribution of a random variable that is derived from a collection of other random variables as follows: first, a random variable is selected by chance from the collection according to given probabilities of selection, and then the value of the selected random variable is realized.

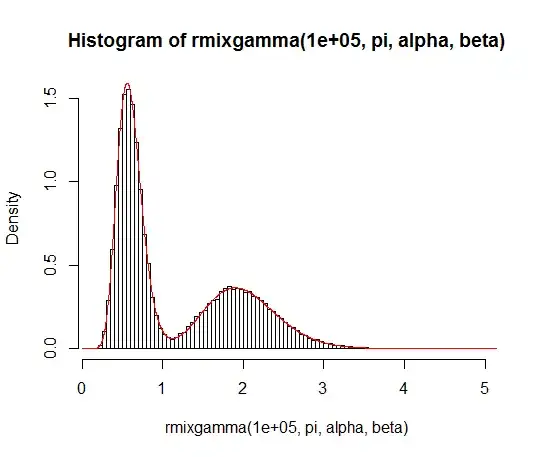
If you know R, this translates to the following example:

# density
dmixgamma <- function(x, pi, alpha, beta) {
  k <- length(pi)
  n <- length(x)
  rowSums(vapply(1:k, function(i) pi[i] * dgamma(x, alpha[i], beta[i]), numeric(n)))
}

# random generation
rmixgamma <- function(n, pi, alpha, beta) {
  k <- sample.int(length(pi), n, replace = TRUE, prob = pi)
  rgamma(n, alpha[k], beta[k])
}

set.seed(123)

pi <- c(4/10, 6/10)
alpha <- c(20, 15)
beta <- c(10, 25)

hist(rmixgamma(1e5, pi, alpha, beta), 100, freq = FALSE)
xx <- seq(0, 10, by = 0.001)
lines(xx, dmixgamma(xx, pi, alpha, beta), col = "red")