1

I am attempting to model the fluorescent signal emitted by a fluorescent calcium indicator (lights up when there is calcium influx into a cell). According to [1], the following formula works as a workable approximation, under certain conditions:

$\Delta F/F = A(1 − e^{−t/\tau_{on}})e^{−t/\tau_{off}}$

$\Delta F/F$ is the change in fluorescence, $t$ is the time since the onset of the signal waveform, $\tau_{on}$ and $\tau_{off}$ represent the rise and decay times respectively; $A$ scales the amplitude of the trace.

My issue is with the two $\tau$s. I was under the impression I could simply plug in appropriate values (e.g. 10 and 1000 ms) for the two $tau$s and I would get a waveform with rise-to-peak and decay-to-baseline times equal to the values of my choice (i.e. also 10 and 1000). This however, doesn't appear to be the case. The wave's rise and decay times each depend on both $\tau$s, such that changing $\tau_{on}$ also affects the decay and vice versa.

My question is: Is it possible to specify exact rise-to-peak, and decay-to-baseline times in the formula above? And if so, how?

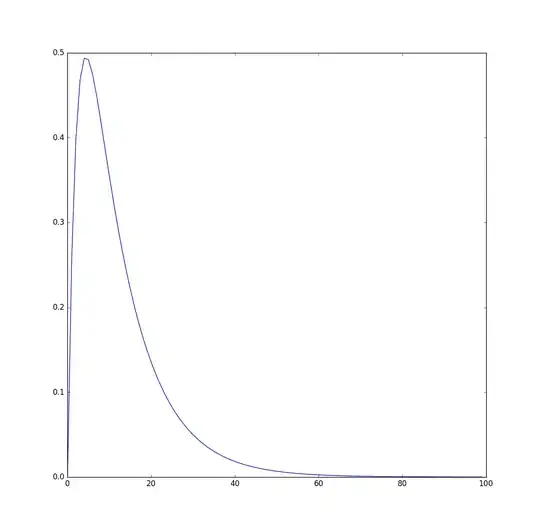
Here's an example I generated with $\tau_{on} = 3$ and $\tau_{off} = 10$ in python. The peak is at 3, and the curve closes in on the baseline around 70, definitely not around 13, which is what I am aiming for.

calcium trace

[1] Lütcke, H., Gerhard, F., Zenke, F., Gerstner, W., & Helmchen, F. (2013). Inference of neuronal network spike dynamics and topology from calcium imaging data. Frontiers in Neural Circuits, 7, 201. http://doi.org/10.3389/fncir.2013.00201

kjetil b halvorsen
  • 77,844
mowe
  • 11
  • 3
  • I think you'll need to be more specific re what you mean by "closes in on the baseline", but, ultimately, just find the peak/baseline for any given values of the two taus, and work backwards to get taus from a given peak/baseline. –  May 01 '16 at 19:39
  • Yes, I wasn't very happy with the "closing in on baseline" formulation myself. However, I wasn't sure if this function (in theory) ever reaches zero again (which is what I meant by baseline). Anyways, the tail seems way to long for a calcium trace. The first actual zero in the numpy array appears somewhere past 7000, and -- as I wrote -- I feel that this may be a mere "artifact" of the way computers represent numbers. – mowe May 02 '16 at 08:15
  • So you say I need to bruteforce this problem; I'm not sure it's feasible, since I don't know what range to check. The combinations that work I found seem very arbitrary to me. – mowe May 02 '16 at 08:24
  • No, I actually meant solve for the taus explicitly using your peak and baseline values, as a formula (unless you discover there isn't one). In general, exponential functions asymptotically approach a value without ever reaching it. –  May 02 '16 at 15:15

1 Answers1

1

This doesn't fully answer your question, but may help.

Since I'm using Mathematica (which dislikes subscripted variable names), I'll substitute $\sigma$ for $\tau _{\text{off}}$ and $\tau$ for $\tau _{\text{on}}$, so your function becomes:

$f(t,\tau ,\sigma ) = A e^{-\frac{t}{\sigma }} \left(1-e^{-\frac{t}{\tau }}\right)$

To find the maximum, we take the derivative (with respect to $t$) and set it equal to 0:

$ \frac{\partial f(t,\tau ,\sigma )}{\partial t} = \frac{A e^{-t \left(\frac{1}{\sigma }+\frac{1}{\tau }\right)} \left(\sigma -\tau e^{t/\tau }+\tau \right)}{\sigma \tau }=0 $

yielding:

$t\to \tau \log \left(\frac{\sigma +\tau }{\tau }\right)$

Note that, in your example, the maximum occurs at $3 \log \left(\frac{13}{3}\right)$, which is about 4.399, not 3.

The value of the function at this $t$ (in other words, the peak value of the function) is:

$ f\left(\tau \log \left(\frac{\sigma +\tau }{\tau }\right),\tau ,\sigma \right)=A \sigma \tau ^{\frac{\tau }{\sigma }} (\sigma +\tau )^{-\frac{\sigma +\tau }{\sigma }} $

If you want the peak to occur at $t=\alpha$ for some value of $\alpha$, you solve:

$\tau \log \left(\frac{\sigma +\tau }{\tau }\right)=\alpha$

to get:

$\sigma \to \tau e^{\alpha /\tau }-\tau$

You can then similarly solve for $\tau$ to get your baseline where you want it.

  • Yes, you're right about the maximum in my example. I neglected the fact that python indexing starts at 0! Thank you for your suggestions, this looks very promising; my math isn't quite where it should be. I'll experiment with this for a bit! – mowe May 03 '16 at 10:45