1

I know there are plenty of questions about the Bias/Variance tradeoff. I've been trying to derive it myself to build some intuition.

I looked at the Wikipedia page, and I saw this: 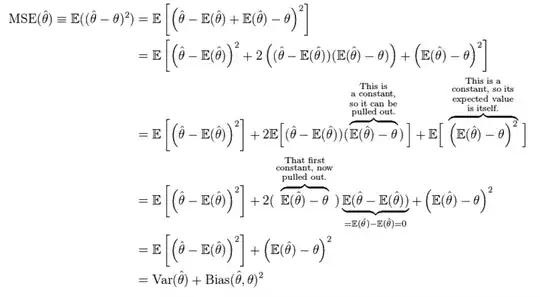bias/variance derivation from wikipedia

Notice where it says "This is a constant...". Which part of the expression E[theta-hat] - theta is constant?

Let's use linear regression as an example, fitting y=mx+b. After fitting a line, the expected value of y at a given value x is constant, sure, because it is just plugging in x into our linear model. But are we talking about the expected value of our model at a particular x, or the expected value of all of the y's predicted by our model (i.e. the sample mean of the y's, y-bar)?

If it is the latter, then this doesn't seem like a constant value to me. The difference between the true model, and the model estimate will vary depending on x. In linear regression, if the difference didn't vary, then the true linear relationship, and our estimate must be parallel.

What are we calling "constant", e.g. in linear regression? I chose linear regression for its ease of illustrating these concepts.

makansij
  • 2,279
  • 9
  • 31
  • 42
  • The key is that although $\theta$ may be unknown, it is constant. And of course, $\mathbb{E}(\hat{\theta})$ is constant. See http://stats.stackexchange.com/questions/123320/mse-decomposition-to-variance-an-bias-square – Mark L. Stone Apr 03 '16 at 22:44
  • It might help a bit for me to get an example of $\theta$. In linear regression, is $\theta$ the true model, y=mx+b from which the values were generated? If so, then I don't understand what we mean by "constant", unless the slope is zero – makansij Apr 03 '16 at 23:04
  • 1
    If m were the true value of the parameter used to generate errored data, then $\theta$ would be m. Or it could be a vector of the combination of m and b. – Mark L. Stone Apr 03 '16 at 23:26
  • OK, thank you. Let's stick with m being our parameter of interest for a bit. So, then why would our estimate of m ever vary? I understand that the expected value of anything is a constant of course. But, in this case it actually seems like there is only one value for m in our model. – makansij Apr 04 '16 at 00:57
  • 2
    m is fixed, i.e., constant, but we don't know what it is, that's why we estimate it. Given a particular estimation procedure (presuming it's not a randomized algorithm), if we repeat the same procedure with the same data, we get the same estimate. But if we repeat it with different data, we can get a different estimate. If we knew m exactly, we could use the estimate of m being m, which has zero variance and zero bias, therefore zero mean square error. – Mark L. Stone Apr 04 '16 at 01:08
  • Okay, I'm starting to understand, thanks so much for your patience @MarkL.Stone. So, the expected value of our estimates of m would be the average of all of estimates during our estimation procedure? And, since ordinary least squares is just a convex optimization problem, there is only one minimum, so there is only one estimate in this case? – makansij Apr 04 '16 at 03:55

0 Answers0