3

I have a question about quasi-likelihood. I think the following formula says something opposite to what likelihood means. Could someone clarify what I'm misunderstanding.

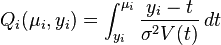
I'm looking at the formula in the page of variance function in Wikipedia . enter image description here

I think this formula says, when the $\mu_i$ and $y_i$ are closer, $Q_i$ becomes smaller. The reason I think like this is that the range of integral is defined by $\mu_i$ and $y_i$, and when they are closer, the range is narrower.

However, this formula represents a kind of likelihood, quasi-likelihood, so my intuition says that when the $\mu_i$ is closer to $y_i$ , quasi-likelihood should be larger, because this situation should be more likely. I'm comparing quasi-likelihood with usual likelihood (used in maximum likelihood). In maximum likelihoods situation, when the observed value and mean are closer, the likelihood is larger.

Could someone clarify the point I'm misunderstanding. Thank you!

P.S. I'm not a math guy and my approach is applied statistics. So easy math explanation is preferable!

stat-hajime
  • 31

1 Answers1

0

$Q_i$ indeed becomes smaller in absolute value when $\mu_i$ and $y_i$ get closer; but the quantity is negative, so it actually gets larger (less negative).

Consider two cases with respect to $\mu_i$ and $y_i$:

  1. $\mu_i\geq y_i$. Then $t$ goes from $y_i$ up to $\mu_i$, $t\geq y_i$, therefore $y_i-t\leq 0$ and you are integrating a negative (or at least non-positive) quantity.
  2. $\mu_i<y_i$. Then let's swap the integration limits: $$\int_{y_i}^{\mu_i}\frac{y_i-t}{\sigma^2V(t)}dt=\int_{\mu_i}^{y_i}\frac{t-y_i}{\sigma^2V(t)}dt.$$ Now $t<y_i$, $t-y_i<0$, and you are again integrating a negative quantity.

When integrating a negative function, the smaller you make the integration range, the larger value you get.