Distribution of the square of a non-standard normal random variable

Question

What is the distribution of the square of a non-standard normal random variable (i.e., the mean is not equal to 0 and the variance is not equal to 1)?

Answer 1

It is a scaled non-central chi-square distribution with one degree of freedom. More specifically, if $Z$ is a normal random variable with mean $\mu$ and variance $\sigma^2$, then $\frac{Z^2}{\sigma^2}$ is a non-central chi-square random variable with one degree of freedom and non-centrality parameter $\lambda=\left(\frac{\mu}{\sigma}\right)^2$.

Answer 2

A noncentral $\chi^2$ distribution, applies only to a normal variable with unit variance. In such case, the square of random variable $X_1\sim N(x|\mu, 1)$ is noncentral $\chi^2$ distributed with degrees of freedom $k=1$ and noncentrality parameter $\lambda=\mu^2$: $$ X_1^2=Z\sim \chi^2(z_1|k, \lambda).$$

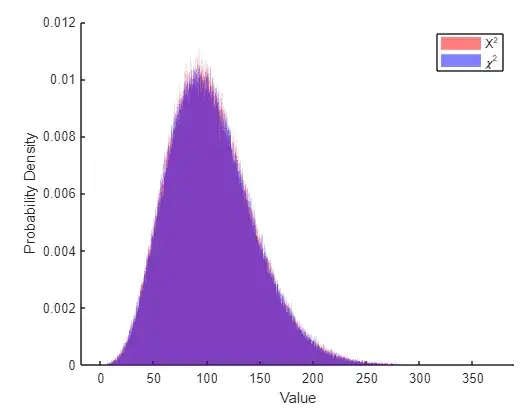
However, one can establish a relationship between a normally distributed variable $X_2 \sim N(x_2|\mu,\sigma)$ and noncentral $Z_2 \sim \chi^2(z_2|1,\tfrac{\mu^2}{\sigma^2})$ distributed variable as such: $$X_2^2=Z\sigma^2$$

Proof by example:

mu = 10;     % Mean of the normal
distribution
sigma = 2;  % Standard deviation of the normal distribution
num_samples = 1000000; % Number of samples
% Generate normal random variables with specified mean and standard deviation
X = normrnd(mu, sigma, num_samples, 1);
% Compute the squares
X_squared = (X).^2;
% Compute non-centrality parameter
lambda = (mu/sigma)^2;
% Generate samples from non-central chi-squared distribution
Y = ncx2rnd(1, lambda, num_samples, 1);
% Plot histograms
figure; hold on;
histogram(X_squared, 'Normalization', 'pdf', 'BinWidth', 0.1, 'FaceColor', 'r', 'FaceAlpha', 0.5, 'EdgeColor','none');
histogram(Y*sigma^2,         'Normalization', 'pdf', 'BinWidth', 0.1, 'FaceColor', 'b', 'FaceAlpha', 0.5, 'EdgeColor','none');
xlabel('Value');
ylabel('Probability Density');
% Add legend
legend('X^2', '\chi^2');

Answer 3

Here is Matlab code showing that the answer by Brent Kerby is not true.

mu = 10;     % Mean of the normal distribution
sigma = 2;  % Standard deviation of the normal distribution
num_samples = 1000000; % Number of samples
% Generate normal random variables with specified mean and standard deviation
X = normrnd(mu, sigma, num_samples, 1);
% Compute the squares
X_squared = X.^2;
% Compute non-centrality parameter
lambda = (mu/sigma)^2;
% Generate samples from non-central chi-squared distribution
Y = ncx2rnd(1, lambda, num_samples, 1);
% Plot histograms
figure; hold on;
histogram(X_squared, 'Normalization', 'pdf', 'BinWidth', 0.1, 'FaceColor', 'r', 'FaceAlpha', 0.5, 'EdgeColor','none');
histogram(Y,         'Normalization', 'pdf', 'BinWidth', 0.1, 'FaceColor', 'b', 'FaceAlpha', 0.5, 'EdgeColor','none');
xlabel('Value');
ylabel('Probability Density');
% Add legend
legend('X^2', '\chi^2');