1

Here is the data:

YEAR   SUM  M   F
 1901   865 672 193
 1902   871 645 226
 1903   875 652 223
 1904   798 575 223
 1905   776 578 198
 1906   795 611 184
 1907   790 618 172
 1908   777 585 192
 1909   702 520 182
 1910   776 596 180
 1911   692 546 146

The additional problems are: 1) Is the number of suicides differing through the years? 2) Is there any difference between males and females?

user1406647
  • 107
  • 6

3 Answers3

3

This sounds like homework, but let me answer with some general principles and ideas:

  • If this is a time series, there should be some kind of time value attached, such as the year or month these occurred in. Where has it gone?
  • As a first step in any data analysis, especially for time series, plot the data. This should help you answer your specific questions 1 and 2.
  • The first column is just the sum of the other two and has no independent role. It might be convenient if you want to do a plot of, say, female suicides as a percentage of the total, which will help you answer your specific question 2.
  • Your data are far too short a time series to do any kind of sophisticated statistical analysis on. A plot is the best you could hope for. If you were to do such analysis (on a longer sample), you would want to have some hypotheses about possible explanators, like unemployment, bankruptcies or some other thing that might drive people to suicide.

  • Before launching into data analysis, ask yourself some questions about how the data are compiled and what their quality are.

    • Is the source of these data trustworthy? Are there other sources, and if so, are the consistent with your data?

    • How are the data compiled? Are you sure you have the full count of case (the population), or is this a sample, an estimate or some other thing?

    • Do the data get revised? If so, does this change how you might view the apparent downward trend in the last few data points?

    • Do the data look plausible relative to data from other sources on, say, total death rates and the total population? For example, if the population is a small village of a few thousand, these numbers might seem implausibly high (though not impossible if there is something special - and tragic - about that village). Conversely, if these data refer to a large population like the United States, they are probably too low and some cases might be being missed.

I hope these suggestions point you in the right direction.

Verbeia
  • 131
  • thank you for answer. I find few interesting points. first i added years, and second that time period is short and plot will be better. Indeed it sounds like homework, but I would like that some explain procedure of time series analysis (step by step) that is the reason I asked for this simple example. Do you know any book like for dummies style? – user1406647 Sep 22 '15 at 07:19
2

A simple to read text is McCleary, R. and R.A. Hay, Jr. Applied Time Series Analysis for the Social Sciences. Beverly Hills and London: Sage, 1980, 328 pp. http://www.alibris.com/search/books/isbn/9780803912052?qwork=23241604 which may be out of print but worth finding. It is certainly not up to date with current methodologies but it is readable and can certainly be a primer. Effective empirical identification of an appropriate ARIMA model (weighted average of the past) depends heavily on the ratio of signal to noise in the history of the data. In my opinion there is never too few observations to construct/estimate a possible model just possibly more difficulty. As more data is used, suggested/refined models can be recursively identified. For example the series 1,9,1,9,1,9,1,9,5,9 contains a strong signal and 1 clearly identifiable anomaly. If one only has the history of the series of interest, one can only identify the auto-projective (ARIMA) structure or some form of deterministic model incorporating pulses/level shifts/seasonal pulses and/or local time trends. Causative models require user-specified possible supporting series.

As a teaching device of what could be done (in a non-causal way) with your three time series, I analyzed your sum series to illustrate the "black art" of ARIMA model identification i.e. identifying the underlying structure purely from the data. Note that ARIMA modelling also encourages user-specification of possible structure given prior knowledge/guess and then tests for necessity/sufficiency. A plot of the original series is here enter image description here . The sample correlations enter image description here suggest an AR(1) model enter image description here whose residuals suggest an anomaly at period 1909 enter image description here . Model refinement augmentation suggested two anomalies (1909 and 1903) in addition to the AR(1) component enter image description here and here enter image description here . Expressed as a simple regression (without the two pulses) we get enter image description here with actual/fit/forecast here enter image description here . All models are wrong .... some are useful ... G.E.P. Box.

Note that the final equation can be restated as y(t)=234+.7*y(t-1)

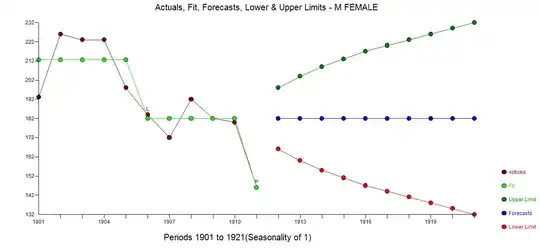I then took the male data and obtained enter image description here and the equation enter image description here while the female data yielded enter image description here and enter image description here

To test the differences between male and female one would use https://en.wikipedia.org/wiki/Chow_test to test the hypothesis of similarity perhaps using a common AR(1) model specification.

IrishStat
  • 29,661
1

I suggest reading the online book of Hyndman and Athanasopoulos "Forecasting: principles and practice". The book explains with details what time series analysis is and how to do it. You may find the book here: https://www.otexts.org/fpp

The book uses R for statistical analyses, so you should have some knowledge of both programming in R and of statistics.

You may find a tutorial on time series analysis here: https://rpubs.com/RatherBit/102453

Here is the Quick-R page on Time series: http://www.statmethods.net/advstats/timeseries.html

At the bottom you'll find a 'Going Further' section, with some online resources for learning time series analysis with R.

This is a CrossValidated page with a lot of additional indications for reading: Books for self-studying time series analysis?

Hope this helps.

Community
  • 1
user3875022
  • 71