Linear OLS v Mixed-Effects Model with Correlated Regressors

Question

Reading this post by @gung brought me to try to reproduce his superb illustrations, and led ultimately to question something I had read or heard, but that I'd like to understand more intuitively: Why is an OLS lm controlling for a correlated variable better (can I say 'better' tentatively?) than a mixed-effects model with different intersects and slopes?

Here's the toy example, again trying to parallel the post quoted above:

First the data:

set.seed(0)    
x1 <- c(rnorm(10,3,1),rnorm(10,5,1),rnorm(10,7,1))
x2 <- rep(c(1:3),each=10)
    y1 <- 2  -0.8 * x1[1:10] + 8 * x2[1:10] +rnorm(10)
    y2 <- 6  -0.8 * x1[11:20] + 8 * x2[11:20] +rnorm(10)
    y3 <- 8  -0.8 * x1[21:30] + 8 * x2[21:30] +rnorm(10)
y <- c(y1, y2, y3)

And the different models:

library(lme4)

fit1 <- lm(y ~ x1)
fit2 <- lm(y ~ x1 + x2)
fit3 <- lmer(y ~ x1 + (1|x2))
fit4 <- lmer(y ~ x1|x2, REML=F)

Comparing Akaike information criterion (AIC) between models:

AIC(fit1, fit2, fit3, fit4)

     df      AIC
     df      AIC
fit1  3 184.5330
fit2  4  97.6568
fit3  4 112.0120
fit4  5 114.8401

So it seems that the best model is lm(y ~ x1 + x2), which I guess make sense given the strong correlation between x1 and x2 cor(x1,x2) [1] 0.8619565.

But the question is, What is the intuition behind this behavior, when the mixed model with varying intercepts and slopes seems to result in coefficients that fit the data beautifully?

coef(lmer(y ~ x1|x2))
$x2

      x1       (Intercept)
1 -1.1595730    11.37746
2 -0.2586303    19.38601
3  0.2829754    24.20038

library(lattice)    
xyplot(y ~ x1, groups = x2, pch=19,
           panel = function(x, y,...) {
             panel.xyplot(x, y,...);
             panel.abline(a=coef(fit4)$x2[1,2], b=coef(fit4)$x2[1,1],lty=2,col='blue');
             panel.abline(a=coef(fit4)$x2[2,2], b=coef(fit4)$x2[2,1],lty=2,col='magenta');
             panel.abline(a=coef(fit4)$x2[3,2], b=coef(fit4)$x2[3,1],lty=2,col='green')
           })

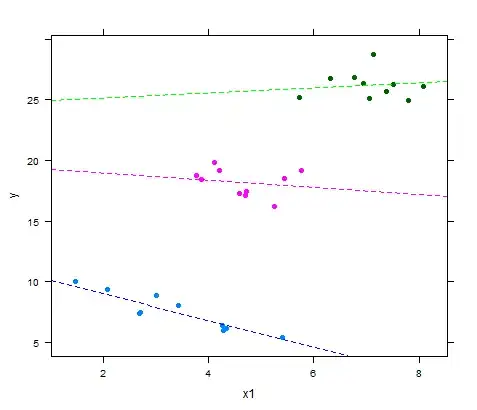
I do realize that the graphical fit of the bivariate OLS can look pretty good as well:

library(scatterplot3d)
plot1 <- scatterplot3d(x1,x2,y, type='h', pch=16,
              highlight.3d=T)
plot1$plane3d(fit2)

... and I don't know if this invalidates the question.

Answer 1

Consistent with the conversation in the comments, it may actually be quite obvious: in mixed-effects, the overall increasing values of $y$ with increasing $x1$ as shown in:

with a positive correlation of cor(x1,y) [1] 0.7924759, is nicely captured in the plane formed by lm(y ~ x1 + x2) (depicted in the OP plots) or in the following graph:

library(car)
library(rgl)
scatter3d (y ∼ x1  +  x2)
rgl.snapshot(filename="scat1.png", fmt="png")

On the other hand, this is simply lost in lmer mixed-effects. Rather than a positive slope in the regression of $y$ over $x1$, all the slope coefficients are consistently negative, because at each level of stratification created by the discrete values of $x2$ (1, 2 and 3), the corresponding $x1$ do slope downwards:

scatter3d (x=x1,y=x2,z=y, groups=as.factor(x2))

(source here)

I tend to assume (and liked to get confirmation) that this may be substantial to the idea of mixed-effects, and that it cannot be corrected by modifying the lmer call synthax. I tried for instance lmer(y ~ (x1|x2), REML=F), lmer(y ~ x1 + (x1|x2), REML=F), among others, with conceptually similar outputs.

Leaving aside the fact that in the example in the OP each of the discrete values that $x2$ assumes as a distinct "unit" role, which is a coercion of the idea of a hierarchical model, where units are typically subjects, it is clear that a lmer mixed-effects model is not optimal in this situation, and that even in the case that the values of $x2$ were more 'natural' units (say, x2==1 corresponded to John; x2==2 was for Tom, and x2==3 were the values for Mary), a linear OLS lm with dummy variables would be more appropriate than a mixed-effects model. From a different perspective, the distribution of the $y$ values along each point in the $x1$ axis does not follow a Gaussian distributions both due to variations between units and within units, as is assumed of mixed-effects models.

As in one of the comments, the mixed-effects model would be more natural in a situation as in the sleepstudy {lme4} database, where different individuals respond to sleep deprivation with progressive increases in reaction time, and the heteroskedasticity seems to increase as times goes on:

require(lme4)
attach(sleepstudy)
fit <- lm(Reaction ~ Days)
plot(fit, pch=19, cex=0.5, col='slategray')

lending itself to fitting different intercepts and slopes for each of the Subjects:

plot(Reaction ~ Days, xlim=c(0, 9), ylim=c(200, 480), type='n', 
     xlab='Days', ylab='Reaction')

for (i in sleepstudy$Subject){
  points(Reaction ~ Days, sleepstudy[Subject==i,], pch=19, 
         cex = 0.5, col=i)
  fit<-lm(Reaction ~ Days, sleepstudy[sleepstudy$Subject==i,])
  a <- predict(fit)
  lines(x=c(0:9),predict(fit), col=i, lwd=1)
}

This model would correspond to the lme4 call lmer(Reaction ~ Days +(Days|Subject)) which would result coef(lmer(Reaction ~ Days +(Days|Subject))) in a different intercept and slope for every subject. On the other hand lmer(Reaction ~ Days +(1|Subject)) would produce different intercepts for each subject, but exactly the same slope for all subjects:

plot(Reaction ~ Days, xlim=c(0, 9), ylim=c(200, 480), type='n', 
     xlab='Days', ylab='Reaction')

for (i in sleepstudy$Subject){
  points(Reaction ~ Days, sleepstudy[Subject==i,], pch=19, 
         cex = 0.5, col=i)
  a<-coef(lmer(Reaction ~ Days + (1|Subject)))$Subject[i,1]
  b<-coef(lmer(Reaction ~ Days + (1|Subject)))$Subject[1,2]
  abline(a=a, b=b, col=i, lwd=1)
}

... clearly not as good a model as the relative AIC values also seem to indicate (AIC(lmer(Reaction ~ Days +(1|Subject)), lmer(Reaction ~ Days +(Days|Subject)) 1794.465 v 1755.628).